I. Newton: ...,,Přitažlivost k Slunci se skládá z přitažlivostí
k jednotlivým částicím Slunce a klesá se vzdalováním od Slunce přesně s druhou
mocninou vzdálenosti až k oběžné dráze Saturna, jak je zřejmé z klidu afélií
planet, a až k nejzazším aféliím komet, jestliže jen jsou ona afélia v klidu``.
Uvedené téma je tradičně zařazováno do tematického celku Gravitační
pole. Proto i náš výklad se bude přidržovat tohoto zaměření.
Odvození přesného tvaru III. Keplerova zákona pro kruhové dráhy lze provést
následovně: Nechť dva hmotné body s hmotnostmi 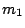 a
a 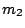 se vzájemně
přitahují a obíhají kolem společného hmotného středu soustavy po kružnicích o
poloměrech
se vzájemně
přitahují a obíhají kolem společného hmotného středu soustavy po kružnicích o
poloměrech 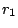 a
a 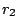 , platí
, platí
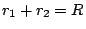 . Podle zákona všeobecné
gravitace můžeme napsat zrychlení značené
. Podle zákona všeobecné
gravitace můžeme napsat zrychlení značené 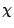 každého z obou hmotných bodů takto:
každého z obou hmotných bodů takto:
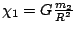 ,
,
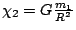 . Úhlová rychlost rotace soustavy kolem hmotného
středu je
. Úhlová rychlost rotace soustavy kolem hmotného
středu je
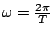 ,
, 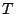 je perioda rotace. Dostředivé zrychlení
píšeme ve tvaru
je perioda rotace. Dostředivé zrychlení
píšeme ve tvaru
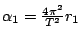 ,
,
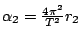 . Srovnáme oba výrazy získané pro
zrychlení
. Srovnáme oba výrazy získané pro
zrychlení
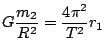 ,
,
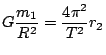 .
Sečtením výrazů na pravých a levých stranách rovnic dostáváme
.
Sečtením výrazů na pravých a levých stranách rovnic dostáváme
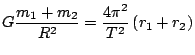 . Úpravou obdržíme
. Úpravou obdržíme
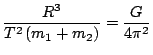 .
Na pravé straně rovnice je konstanta, tedy výraz na levé straně platí pro libovolnou soustavu dvou hmotných bodů, které se vzájemně přitahují podle zákona všeobecné gravitace a obíhají rovnoměrným pohybem po kruhových drahách kolem společného hmotného středu. Vztah platí i obecně, pro pohyb po eliptických drahách.
.
Na pravé straně rovnice je konstanta, tedy výraz na levé straně platí pro libovolnou soustavu dvou hmotných bodů, které se vzájemně přitahují podle zákona všeobecné gravitace a obíhají rovnoměrným pohybem po kruhových drahách kolem společného hmotného středu. Vztah platí i obecně, pro pohyb po eliptických drahách.
Uvažujme dvě takové dvojice hmotných bodů, nechť 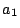 ,
, 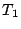 ,
, 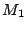 ,
, 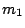 jsou parametry první dvojice a
jsou parametry první dvojice a 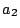 ,
, 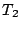 ,
, 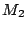 ,
, 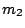 druhé dvojice.
druhé dvojice.
III. Keplerův zákon spojuje dvě nezávislé dvojice soustavy, z nichž každá se skládá z centrálního a druhého tělesa (družice,měsíce) obíhajícího kolem.
Přesný tvar III. Keplerova zákona má pro obě dvojice hmotných bodů
tvar
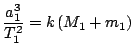 , ,
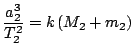 .
Podělením rovnic získáme používaný vztah pro přesný tvar III. Keplerova zákona .
Podělením rovnic získáme používaný vztah pro přesný tvar III. Keplerova zákona
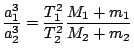 . Připomínáme,
že v uvedeném vztahu hmotnost centrálního tělesa je . Připomínáme,
že v uvedeném vztahu hmotnost centrálního tělesa je 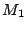 , hmotnost družice , hmotnost družice
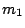 , velká poloosa dráhy družice je , velká poloosa dráhy družice je 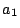 , její oběžná doba , její oběžná doba 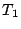 . Analogické veličiny druhé soustavy jsou označeny indexem 2. . Analogické veličiny druhé soustavy jsou označeny indexem 2.
|
|
V astronomických měřítcích lze hvězdy a planety považovat za hmotné body s dostatečnou přesností, proto odvozené vztahy platí obecně pro pohyb těchto těles v kosmickém prostoru.
III. Keplerův zákon je jedinou klasickou přímou metodou určování hmotností
kosmických těles. Známe-li hmotnost jednoho centrálního tělesa, můžeme
z kinematických charakteristik dvou soustav stanovit hmotnost centrálního tělesa
druhé soustavy. Nejprve metodu použil Newton v Principiích, kdy stanovil
relativní hmotnost Jupitera vzhledem k Slunci na základě údajů o oběhu měsíce
Kallisto. Později, po stanovení hodnoty gravitační konstanty 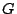 , tato metoda umožňovala určovat hmotnosti planet z pohybu jejich měsíců.
, tato metoda umožňovala určovat hmotnosti planet z pohybu jejich měsíců.
Vhodné úlohy jsou následující:
Úloha 1
Oběžná doba Měsíce kolem Země je přibližně
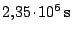 , zhruba 27,3 dne.
Určete poloměr dráhy a oběžnou rychlost pohybu Měsíce kolem Země. Známe
, zhruba 27,3 dne.
Určete poloměr dráhy a oběžnou rychlost pohybu Měsíce kolem Země. Známe
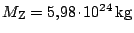 ,
,
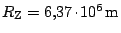 .
.
Řešení:
Poloměr dráhy určíme ze vztahu
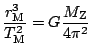 , odtud
, odtud
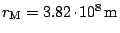 . Oběžnou rychlost stanovíme ze vztahu
. Oběžnou rychlost stanovíme ze vztahu
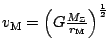 , tedy
, tedy
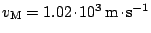 .
.
III. Keplerův zákon v jednoduchém tvaru
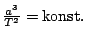 lze aplikovat na různé soustavy s odlišnými centrálními tělesy, např. Sluncem, planetami, Zemí. Hodnota konstanty je tudíž pro různé soustavy odlišná.
lze aplikovat na různé soustavy s odlišnými centrálními tělesy, např. Sluncem, planetami, Zemí. Hodnota konstanty je tudíž pro různé soustavy odlišná.
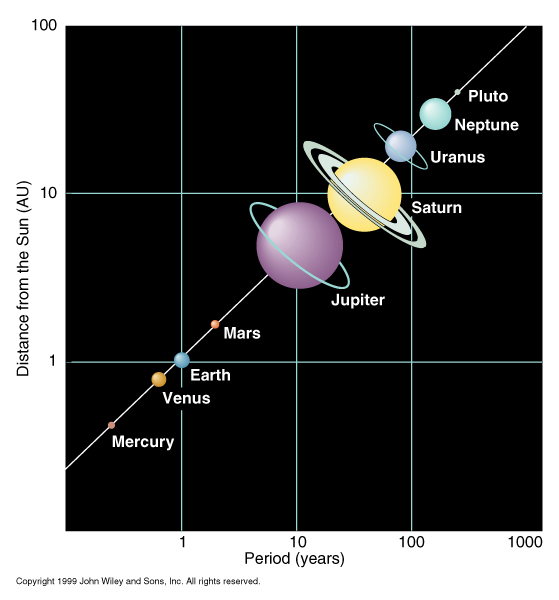
Tabulka velikostí velkých poloos drah a oběžných dob planet
| Planeta |
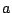 [AU] [AU] |
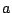 [ [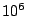 km] km] |
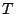 [roky] [roky] |
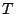 [dny] [dny] |
| Merkur |
0,387 |
57,909 |
0,241 |
87,97 |
| Venuše |
0,723 |
108,209 |
0,615 |
224,70 |
| Země |
1,000 |
149,598 |
1,000 |
365,26 |
| Mars |
1,524 |
227,937 |
1,881 |
686,98 |
| Jupiter |
5,203 |
778,412 |
11,857 |
4332,59 |
| Saturn |
9,537 |
1426,725 |
29,423 |
10759,22 |
| Uran |
19,191 |
2870,972 |
83,747 |
30685,4 |
| Neptun |
30,069 |
4498,253 |
163,723 |
59800 |
| Pluto |
39,481 |
5906,376 |
248,021 |
90584 |
Na adrese http://www.star.ucl.ac.uk/~idh/1B11/kepler/kepler.html lze nalézt demonstraci Keplerových zákonů.
Vypočtěme hodnotu
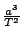 například pro Zemi a Mars. V obou případech obdržíme
po převedení do SI přibližně hodnotu
například pro Zemi a Mars. V obou případech obdržíme
po převedení do SI přibližně hodnotu
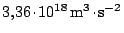 . Ověřte výpočtem u jednotlivých planet platnost
vztahu
. Ověřte výpočtem u jednotlivých planet platnost
vztahu
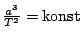 .
.
Soustava galileovských měsíců Jupitera
| Měsíc |
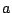 [ [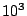 km] km] |
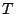 [dny] [dny] |
| Io |
422 |
1,769 |
| Europa |
671 |
3,551 |
| Ganymede |
1070 |
7,155 |
| Kallisto |
1883 |
16,689 |
V případě soustavy měsíců Jupitera obdržíme po převedení do SI hodnotu
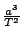 přibližně
přibližně
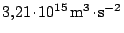 .
.
Soustava vybraných měsíců Saturna
| Měsíc |
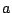 [ [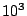 km] km] |
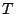 [dny] [dny] |
| Tethys |
294,66 |
1,888 |
| Rhea |
527,04 |
4,517 |
| Titan |
1221,83 |
15,945 |
V případě soustavy měsíců Saturna obdržíme po převedení do SI
hodnotu
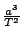 přibližně
přibližně
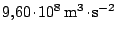 .
.
Vypouštění umělých družic se v současné době provádí prostřednictvím vícestupňových raket, jejichž poslední stupeň obsahuje družici. Po startu se raketa pohybuje několik minut tahem raketového motoru, v tzv. aktivní části letu. Z počátku kolmo vzhůru, aby se co nejrychleji dostala z nejhustších vrstev atmosféry. Postupně se dráha zakřivuje a raketa se natáčí stále více k horizontálnímu směru, přičemž získává větší rychlost. Při horizontálním letu potřebuje ke zvýšení rychlosti na danou hodnotu nejméně energie a tudíž má nejmenší spotřebu paliva. Vyplývá to z faktu, že při tomto pohybu je síla přitažlivosti kolmá na směr pohybu rakety. Pokud by se teoreticky pohybovala neustále vertikálním směrem, energie rakety by se nespotřebovávala pouze na zvýšení rychlosti, ale také na překonávání zemské přitažlivosti.
Po vyčerpání paliva motorem posledního stupně začíná pasivní pohyb po dráze kolem Země. Obvykle se družice odděluje od nosné rakety a tento moment je pokládán za vstup umělé družice na oběžnou dráhu kolem Země. Družice se pohybuje podle zákonů kosmické mechaniky pod vlivem přitažlivosti Země a druhých kosmických těles, pouze na úkor energie získané při aktivní části letu.
V prvním přiblížení se družice pohybuje po eliptické dráze, jež nemění svoji polohu v prostoru, ohnisko elipsy je ve středu Země. Jde o tzv. ideální pohyb družice, při kterém předpokládáme, že na pohybující se družici působí pouze přitažlivá centrální síla gravitačního pole Země.
Pro družici pohybující se rychlostí
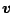 po elipse ve vzdálenosti
po elipse ve vzdálenosti
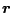 od středu Země, jestliže zanedbáme ztráty vlivem tření, platí zákon zachování mechanické energie
od středu Země, jestliže zanedbáme ztráty vlivem tření, platí zákon zachování mechanické energie
kde
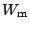 je mechanická energie,
je mechanická energie,
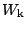 je kinetická energie,
je kinetická energie,
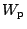 je potenciální energie,
je potenciální energie,
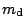 je hmotnost družice,
je hmotnost družice, 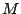 je
hmotnost Země a
je
hmotnost Země a 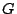 je gravitační konstanta.
je gravitační konstanta.
Rovnice platí v libovolném bodě dráhy družice, tedy i v apogeu a perigeu.
kde
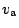 je rychlost v apogeu,
je rychlost v apogeu,
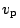 je rychlost v perigeu,
je rychlost v perigeu,
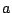 je velikost hlavní poloosy,
je velikost hlavní poloosy,
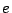 je excentricita elipsy,
je excentricita elipsy,
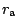 je vzdálenost družice od středu Země
v apogeu,
je vzdálenost družice od středu Země
v apogeu,
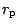 je vzdálenost v perigeu. Podle II. Keplerova zákona platí
je vzdálenost v perigeu. Podle II. Keplerova zákona platí
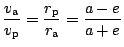 .
Dosadíme a upravíme
.
Dosadíme a upravíme
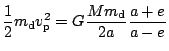 . Pro
mechanickou energii obdržíme
. Pro
mechanickou energii obdržíme
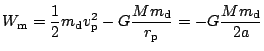 . Zobecněný vztah má
tvar
. Zobecněný vztah má
tvar
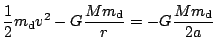 .
Odtud dostáváme důležitý vztah pro rychlost pohybu družice
.
Odtud dostáváme důležitý vztah pro rychlost pohybu družice
![$ \displaystyle
v=\left[GM\left(\frac{2}{r}-\frac{1}{a}\right)\right]^{\frac{1}{2}}$](img201.gif) . Rychlost družice při
dané vzdálenosti
. Rychlost družice při
dané vzdálenosti 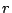 od středu Země závisí pouze na velikosti hlavní poloosy dráhy, nikoliv na jejím tvaru. Provedeme diskusi vztahu vzhledem k možným tvarům dráhy a rychlosti pohybu.
od středu Země závisí pouze na velikosti hlavní poloosy dráhy, nikoliv na jejím tvaru. Provedeme diskusi vztahu vzhledem k možným tvarům dráhy a rychlosti pohybu.
- Pro
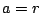 je dráha kruhová a pro její rychlost platí
je dráha kruhová a pro její rychlost platí
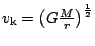 . Jestliže položíme
. Jestliže položíme
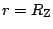 dostaneme hodnotu I. kosmické rychlosti
dostaneme hodnotu I. kosmické rychlosti
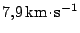 .
.
- Pro
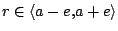 je dráha družice eliptická a její
rychlost je dána vztahem
je dráha družice eliptická a její
rychlost je dána vztahem
![$ \displaystyle v_\mathrm{e}
=\left[GM\left(\frac{2}{r}-\frac{1}{a}\right)\right]^{\frac{1}{2}}$](img207.gif) .
.
- Pro
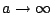 se družice pohybuje po parabolické dráze
a pro její rychlost platí
se družice pohybuje po parabolické dráze
a pro její rychlost platí
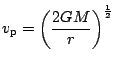 .
Položíme-li
.
Položíme-li
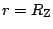 obdržíme hodnotu II. kosmické rychlosti
obdržíme hodnotu II. kosmické rychlosti
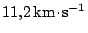 .
.
Důležitá je také sestupná fáze pohybu družice, kdy se pohybuje v zemské
atmosféře. Největší odpor klade atmosféra v perigeu, což vede ke snížení
rychlosti
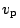 . V důsledku toho družice snižuje výšku apogea, tudíž
je relativně vyšší hodnota rychlosti
. V důsledku toho družice snižuje výšku apogea, tudíž
je relativně vyšší hodnota rychlosti
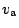 . Při snižování výšky dráhy zvětšuje družice svoji průměrnou rychlost a pohybuje se neustále rychleji. V sestupné fázi letu při přechodu do relativně hustších vrstev atmosféry v důsledku odporu atmosféry paradoxně narůstá průměrná rychlost na oběžné dráze. Výklad paradoxu lze vést ze zákona zachování mechanické energie
. Při snižování výšky dráhy zvětšuje družice svoji průměrnou rychlost a pohybuje se neustále rychleji. V sestupné fázi letu při přechodu do relativně hustších vrstev atmosféry v důsledku odporu atmosféry paradoxně narůstá průměrná rychlost na oběžné dráze. Výklad paradoxu lze vést ze zákona zachování mechanické energie
Pro zjednodušení dalších úvah, nechť se pohyb družice děje po kruhové dráze
s rychlostí
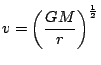 . Po dosazení do vztahu pro mechanickou
energii obdržíme
. Po dosazení do vztahu pro mechanickou
energii obdržíme
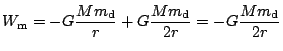 .
.
Bržděním v atmosféře dochází k přeměně části mechanické energie na teplo,
velikost mechanické energie klesá. Vzhledem k tomu, že v absolutní hodnotě je
kinetická energie 2krát menší než potenciální energie, dochází k růstu
kinetické energie a tedy narůstá průměrná rychlost pohybu družice. Poloměr
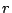 dráhy klesá, družice postupně sestupuje do stále hustších vrstev
atmosféry. Ve výšce zhruba
dráhy klesá, družice postupně sestupuje do stále hustších vrstev
atmosféry. Ve výšce zhruba 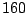 km je odpor atmosféry již takový, že družice nemůže vykonat více než jeden oběh kolem Země a shoří. Pro pochopení problematiky navádění družic na eliptickou dráhu je vhodná úloha:
km je odpor atmosféry již takový, že družice nemůže vykonat více než jeden oběh kolem Země a shoří. Pro pochopení problematiky navádění družic na eliptickou dráhu je vhodná úloha:
Úloha 1
Umělá družice se pohybuje po kruhové dráze nad Zemí ve výšce 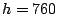 km. Je třeba ji převést na eliptickou dráhu s maximální
vzdáleností od povrchu
km. Je třeba ji převést na eliptickou dráhu s maximální
vzdáleností od povrchu
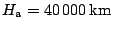 a minimální
vzdáleností
a minimální
vzdáleností
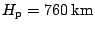 . Stanovte hodnotu nezbytné změny rychlosti družice při jejím převedení na zamýšlenou dráhu. Určete velikost oběžné doby družice na nové dráze.
. Stanovte hodnotu nezbytné změny rychlosti družice při jejím převedení na zamýšlenou dráhu. Určete velikost oběžné doby družice na nové dráze.
Řešení:
Předpokládejme, že změna rychlosti družice proběhne za velmi krátký časový interval ve srovnání s velikostí oběžné doby.
Nalezneme
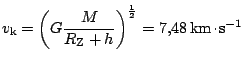 ,
dále
,
dále
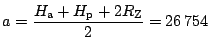 km. Rychlost na eliptické dráze je
km. Rychlost na eliptické dráze je
![$ \displaystyle v_\mathrm{p}
=\left[GM\left(\frac{2}{r}-\frac{1}{a}\right)\right]^{\frac{1}{2}}=
9,84\,\mathrm{km}\kern -1.2pt \cdot\kern -1.2pt \mathrm{s}^{-1}$](img219.gif) ,
,
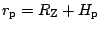 . Tudíž
. Tudíž
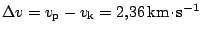 . Velikost oběžné doby
na
eliptické dráze je rovna
. Velikost oběžné doby
na
eliptické dráze je rovna
![$ \displaystyle
T_\mathrm{p}=T_\mathrm{k}\left[\frac{2R_\mathrm{Z}+H_\mathrm{p}+...
...\left(R_\mathrm{Z}+H_\mathrm{p}\right)}\right]^{\frac{3}{2}}=12,1\,\mathrm{hod}$](img222.gif) .
.
Nejjednodušším z mimozemských letů je let na Měsíc, kdy kosmická sonda či loď s lidskou posádkou po výstupu z oblasti přitažlivosti Země ihned vstupuje do oblasti přitažlivosti Měsíce.
Teoreticky za zjednodušujícího předpokladu oběžné kruhové dráhy Měsíce můžeme rozdělit možné dráhy k dosažení Měsíce na tři základní typy podle směru startovací rychlosti:
- Vertikální směr vektoru startovací rychlosti odpovídá drahám přímkovým.
- Druhý typ dráhy dostaneme v případě, jestliže vektor startovací rychlosti svírá určitý úhel s horizontem.
- Při horizontálním směru vektoru startovací rychlosti obdržíme třetí typ drah.
Pro všechny uvedené typy drah je prakticky stejná startovací rychlost
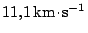 . Z výpočtů vyplývá, že doba letu na Měsíc závisí pouze na velikosti vektoru startovací rychlosti, nikoliv na jeho směru.
. Z výpočtů vyplývá, že doba letu na Měsíc závisí pouze na velikosti vektoru startovací rychlosti, nikoliv na jeho směru.
V praxi se nejprve vypouští raketa na kruhovou parkovací dráhu kolem Země, ze které následně startuje kosmická sonda k Měsíci.
V dalším výkladu je účelné seznámit žáky s významem rychlosti kosmické sondy pro dosažení Měsíce respektive jejím přistáním na povrchu Měsíce případně vytvoření umělé družice tohoto tělesa.
Pro žáky je pochopitelné, že pro dosažení Měsíce jsou použitelné rychlosti
větší než II. kosmická rychlost. Lety k Měsíce jsou však možné i s menšími
rychlostmi
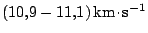 , při kterých se
kosmické sondy pohybují po eliptických drahách s velkými excentricitami.
Rovněž je nutné vyvrátit žákům nesprávnou domněnku, že kosmická sonda celou
dráhu k Měsíci proletí startovací rychlostí, t.j, zhruba
, při kterých se
kosmické sondy pohybují po eliptických drahách s velkými excentricitami.
Rovněž je nutné vyvrátit žákům nesprávnou domněnku, že kosmická sonda celou
dráhu k Měsíci proletí startovací rychlostí, t.j, zhruba
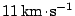 .
.
V této souvislosti je vhodné objasnit, že přitažlivost Země během letu
zmenšuje rychlost kosmické sondy, jejíž hodnota při vstupu do oblasti
přitažlivosti Měsíce se snižuje na
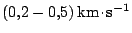 . Po překročení oblasti přitažlivosti
Měsíce se obvykle za vztažnou soustavu bere soustava spojená s Měsícem, takže
je třeba od geocentrické rychlosti sondy vektorově odečíst geocentrickou
rychlost Měsíce, tj. zhruba
. Po překročení oblasti přitažlivosti
Měsíce se obvykle za vztažnou soustavu bere soustava spojená s Měsícem, takže
je třeba od geocentrické rychlosti sondy vektorově odečíst geocentrickou
rychlost Měsíce, tj. zhruba
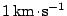 . Při měkkém
přistání na Měsíci se tato rychlost vzhledem k povrchu Měsíce musí anulovat
brzdícím motorem. Z výše uvedených důvodů proto doba letu Země - Měsíc není
10 hodin, jak by tomu bylo při konstantní rychlosti kosmické sondy
. Při měkkém
přistání na Měsíci se tato rychlost vzhledem k povrchu Měsíce musí anulovat
brzdícím motorem. Z výše uvedených důvodů proto doba letu Země - Měsíc není
10 hodin, jak by tomu bylo při konstantní rychlosti kosmické sondy
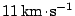 , ale přibližně 3 dny.
, ale přibližně 3 dny.
Při vyvedení kosmické sondy na kruhovou dráhu kolem Měsíce se rychlost musí
snížit brzdícím motorem na
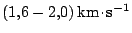 , v závislosti na vybrané dráze.
, v závislosti na vybrané dráze.
Na Měsíci, jehož hmotnost je zhruba 81krát menší než hmotnost Země a jehož
poloměr je asi 3,7krát menší než poloměr Země, je gravitační zrychlení
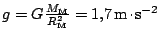 . Pro
I. kosmickou rychlost na Měsíce dostaneme
. Pro
I. kosmickou rychlost na Měsíce dostaneme
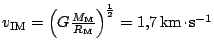 .
II. kosmická rychlost má hodnotu
.
II. kosmická rychlost má hodnotu
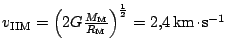 .
.
V současné době jsme svědky intenzivního průzkumu Marsu, jehož strategickým cílem je příprava budoucího přistání lidské posádky. Proto jsou v současné době získávány informace o fyzikálních a chemických podmínkách v atmosféře i na povrchu Marsu. Cílem následujícího výkladu je žákům odpovědět na otázku, jak se kosmické sondy k Marsu dostávají.
Jednoduchá novinářská odpověď je nasnadě - po meziplanetárním letu, který trvá zpravidla osm až devět měsíců. Žákům je však účelné podat hlubší fyzikální vysvětlení. Především je třeba objasnit principiální rozdílnost pohybu v meziplanetárním prostoru od pohybu v zemském ovzduší, který znají z mechaniky či běžného občanského života. Stručně proto budeme základní rozdíly charakterizovat na jednoduchých příkladech.
První a nejpodstatnější odlišnost je v použití a spotřebě energie. Při letu v kosmickém prostoru téměř neexistuje odpor prostředí a spotřeba energie závisí prakticky pouze na směru startu ze Země a úpravách dráhy v meziplanetárním prostoru. Provedeme přibližné srovnání: U letu letadla zemskou atmosférou nezáleží na směru, kterým se pohybuje, spotřeba energie je stále stejná, za předpokladu konstantních podmínek v atmosféře. Naopak kosmické sondy vypouštěné ve směru pohybu Země kolem Slunce spotřebují přibližně 3krát méně energie než při vypouštění proti směru pohybu Země. Poněvadž planety včetně Země obíhají kolem Slunce ve stejném smyslu, většina klasických kosmických sond letící k jiným planetám se z tohoto důvodu pohybuje v tomto smyslu.
Nejvýhodnější meziplanetární dráhy z hlediska spotřeby energie jsou tzv.
poloeliptické. Velké osy těchto drah procházejí Sluncem, které leží v jednom
z ohnisek. Nejbližší bod této dráhy ke Slunci - perihélium, perihel, přísluní
- je na dráze Země a odtud tedy sonda startuje; nejvzdálenější bod - afélium,
afel, odsluní - je na dráze cílové planety. V praxi při letech kosmických sond jsou vybírány takové dráhy, které se málo liší od poloeliptických. Malá chyba ve startovací rychlosti vede k velké odchylce skutečné dráhy kosmické sondy od propočítané a pak je nutné při letu provádět více korekčních manévrů.
Setkání kosmické sondy s cílovou planetou, v našem případě s Marsem, dovolí
pouze takový termín startu, kdy polohu Země při startu a Marsu při setkání
spojuje realizovatelná, v zásadě poloeliptická, dráha. To je velmi obtížné,
jestliže si uvědomíme, že jak místo startu - Země, tak i cíl - Mars jsou
v pohybu. Vlivem rozdílné střední oběžné rychlosti pohybu Země
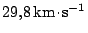 a Marsu
a Marsu
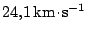 a jejich odlišné vzdálenosti od Slunce, se nepřetržitě mění i jejich vzájemná poloha v prostoru.
a jejich odlišné vzdálenosti od Slunce, se nepřetržitě mění i jejich vzájemná poloha v prostoru.
Podmínka jednoznačného určení poloh Země a Marsu dává vhodný okruh dat startu a setkání výhodných z hlediska spotřeby energie kosmické sondy. Optimální doba pro start k letu na Mars je během každých dvou let zhruba 50 dnů.
Druhý rozdíl mezi pohybem na Zemi a v meziplanetárním prostoru spočívá ve
vlivu tření. Při pohybu na Zemi, například při zastavování automobilu, je možné
prostým vypnutím motoru automobil zastavit, neboť vlivem odporu prostředí
a tření se zastaví sám. V meziplanetárním prostoru téměř neexistuje odpor
prostředí, a tudíž rychlost kosmické sondy přibližující se k cílové planetě musí
být shodná s rychlostí této planety. Přitom je nepodstatné, která z obou
rychlostí je větší, neboť v obou případech je nutné k dosažení planety vynaložit
další energii. Jestliže se cílová planeta pohybuje rychleji než kosmická sonda,
je třeba zvýšit rychlost k ,,dohnání`` planety. Naopak jestliže cílová planeta
se pohybuje pomaleji, je nutno kosmickou sondu ,,zbrzdit`` Obecně tedy při
meziplanetárním letu je fakticky nutná dvojí spotřeba energie, jak při uvedení
kosmické sondy do pohybu, tak při ,,stíhání`` respektive ,,brzdění`` u cílové planety.
Dráhy v meziplanetárním prostoru se rozprostírají na stovky milionů kilometrů, což vyžaduje speciální požadavky na velikost a směr při navedení na meziplanetární dráhu. Velká vzdálenost planet a jejich relativně malé rozměry ztěžují přesné přílety kosmických sond k planetám. Jak jsme se již zmiňovali, jsou nutné korekční manévry, které jsou nezbytné pro přesný let sondy. Tak například v případě letu kosmické sondy Mars Pathfinder byly provedeny v lednu, únoru, květnu a červnu 1997 čtyři korekční manévry. Bez přesné znalosti mechaniky kosmického letu by nebylo možné realizovat rozsáhlý a náročný program, kterým nesporně celý projekt výzkumu Marsu je.
Přejděme nyní k rozboru konkrétního letu ze Země na Mars. Vyjdeme ze zjednodušujícího předpokladu, že dráhy Země i Marsu kolem Slunce jsou kruhové a leží v jedné rovině. Nejprve je třeba určit minimální rychlost, kterou kosmická sonda musí dosáhnout, aby se vzdálila z oblasti aktivity Země a směřovala po dráze směrem k Marsu.
Pojem oblast aktivity planety, v našem případě Země, je pro žáky poměrně
obtížný, matematické odvození definiční nerovnice je uváděno až na vysokoškolské
úrovni. Oblastí aktivity, u nás nepřesně nazývané sférou aktivity, ale o
sférický tvar jde pouze přibližně, nazýváme množinu všech bodů v prostoru kolem
planety, pro které platí, že poměr rušícího zrychlení udílenému kosmické sondě
planetou
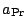 ku zrychlení udílenému Sluncem
ku zrychlení udílenému Sluncem
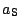 je větší než
poměr rušícího zrychlení udílenému Sluncem sondě
je větší než
poměr rušícího zrychlení udílenému Sluncem sondě
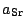 ku zrychlení,
udílenému sondě planetou
ku zrychlení,
udílenému sondě planetou
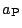 , tedy
, tedy
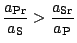 .
.
Jinak řečeno: uvnitř oblasti aktivity planeta ,,ruší`` pohyb vztahovaný ke Slunci
více než ,,ruší`` Slunce pohyb vztahovaný k planetě. Uvnitř oblasti aktivity planety vzhledem k Slunci převládá vliv planety nad rušivým působením Slunce. Proto uvnitř oblasti aktivity vztahujeme pohyb kosmických sond k planetám jako k hlavnímu centrálnímu tělesu, Slunce chápeme jako rušící těleso.
Vraťme se k našemu výkladu. Heliocentrická rychlost k dosažení Marsu má hodnotu
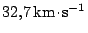 . Země se pohybuje po dráze střední oběžnou
rychlostí
. Země se pohybuje po dráze střední oběžnou
rychlostí
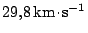 , nutná rychlost kosmické sondy při
opouštění oblasti aktivity Země, sahající do vzdálenosti přibližně
, nutná rychlost kosmické sondy při
opouštění oblasti aktivity Země, sahající do vzdálenosti přibližně
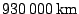 , je dána rozdílem obou rychlostí, tedy
, je dána rozdílem obou rychlostí, tedy
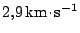 . Minimální počáteční tzv. startovací rychlost
z povrchu Země je určena vztahem
. Minimální počáteční tzv. startovací rychlost
z povrchu Země je určena vztahem
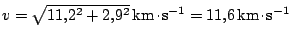 , kde
, kde
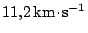 je hodnota druhé kosmické rychlosti.
je hodnota druhé kosmické rychlosti.
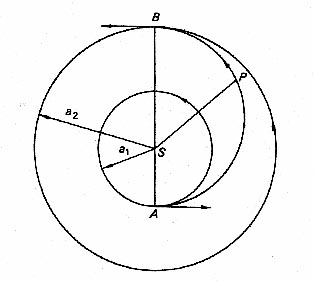
Dráhy s potřebnou minimální energií jsou tzv. hohmannovské dráhy, nazývané na
počest německého matematika a fyzika Waltera Hohmanna (1880-1943). Přechod ze
Země ( ) k Marsu (
) k Marsu (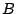 ) se uskutečňuje po poloeliptické přechodové dráze,
velikost jejíž velké poloosy vypočítáme v souladu s předchozím obrázkem takto:
) se uskutečňuje po poloeliptické přechodové dráze,
velikost jejíž velké poloosy vypočítáme v souladu s předchozím obrázkem takto:
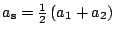 . Excentricitu přechodové dráhy určíme ze
vztahu
. Excentricitu přechodové dráhy určíme ze
vztahu
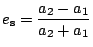 . Dobu letu získáme
z III. Keplerova zákona
. Dobu letu získáme
z III. Keplerova zákona
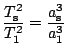 , což po dosazení dá
hodnotu
, což po dosazení dá
hodnotu
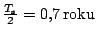 .
.
Heliocentrickou rychlost kosmické sondy obdržíme výpočtem
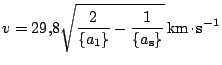 ,
vzdálenosti
,
vzdálenosti 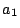 ,
,
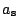 dosazujeme v astronomických jednotkách.
dosazujeme v astronomických jednotkách.
Přejděme od zjednodušeného idealizovaného letu k reálnému, při kterém přihlížíme
k eliptičnosti drah planet. V tom případě je vhodné, aby se v okamžiku startu
nacházela Země v perihéliu své dráhy, kde je rychlost planety asi o
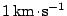 vyšší než v aféliu a má hodnotu
vyšší než v aféliu a má hodnotu
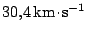 . Vyšší startovací rychlost umožňuje zkrácení dráhy letu a také výhodnější kratší rádiové spojení s případnými přistávacími moduly v okamžiku přiblížení a přistání kosmických lodí, neboť Mars je v menší vzdálenosti od Země.
. Vyšší startovací rychlost umožňuje zkrácení dráhy letu a také výhodnější kratší rádiové spojení s případnými přistávacími moduly v okamžiku přiblížení a přistání kosmických lodí, neboť Mars je v menší vzdálenosti od Země.
Na ukázku uvedeme údaje z letu kosmické sondy nesoucí na palubě Mars Pathfinder. Přechodová dráha, blížící se hohmannovské, měla následující hodnoty oskulačních elementů:
| velká poloosa dráhy |
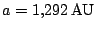 ; ; |
| numerická excentricita |
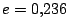 ; ; |
| sklon dráhy |
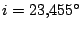 ; ; |
| oběžná doba |
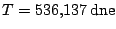 . . |
Připomínáme, že oskulačními elementy rozumíme elementy propočítané pro oskulační dráhu v daný časový okamžik. Oskulační dráha je trajektorie, po níž by se kosmická sonda pohybovala, pokud bychom uvažovali od daného časového okamžiku pouze gravitační vliv Slunce.
Pro detailnější demonstraci průběhu letu uvádíme hodnoty heliocentrické rychlosti a vzdálenosti výše uvedené kosmické sondy, je patrný pokles rychlosti při přibližování k Marsu:
| Datum |
Heliocentrická vzdálenost [km] |
Heliocentrická rychlost
[
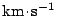 ] ] |
| 1. 1. 1997 |
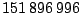 |
32,583 |
| 1. 2. 1997 |
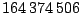 |
30,462 |
| 1. 3. 1997 |
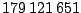 |
28,195 |
| 1. 4. 1997 |
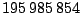 |
25,835 |
| 1. 5. 1997 |
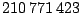 |
23,926 |
| 1. 6. 1997 |
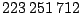 |
22,406 |
| 1. 7. 1997 |
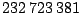 |
21,377 |
Kosmická sonda nesoucí na palubě Mars Pathfinder uletěla na své dráze od
3. prosince 1996 do 4. července 1997, kdy přistála na Marsu,
203 miliónů kilometrů. V okamžiku přistání v oblasti Ares Vallis byla její
vzdálenost od Slunce 233 milionů km a od Země 191 milionů km. Její
heliocentrická rychlost před přistávacím manévrem byla
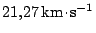 .
.
Poznámka: Mars Pathfinder 6. července 1997 opustil mobilní robot Sojourner
(dočasný obyvatel) - automatické šestikolové vozítko o hmotnosti přibližně
10 kg, které provádělo mimo jiné chemickou analýzu povrchových hornin. Vedle
toho bylo každodenně zkoumáno počasí, například 7. srpna 1997 byl zjištěn tlak
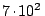 Pa, teplota
Pa, teplota
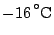 , slabý západní vítr.
, slabý západní vítr.
Výstižně J. Grygar v roce 2001 shrnul, že Mars je planeta se záhadnou minulostí a perspektivní budoucností. Ta je spojena s předpokládanou existencí vody, nalézající se s velkou pravděpodobností pod povrchem v hloubkách několika desítek až set metrů. Planeta je předmětem výzkumu jak dalších kosmických sond, tak rovněž přímého pozorování. Při velké opozici v srpnu 2003 při vzdálenosti od Země pouze 56 milionů kilometrů byly příznivé podmínky pro pozorování povrchu Marsu.
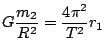 ,
,
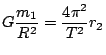 .
Sečtením výrazů na pravých a levých stranách rovnic dostáváme
.
Sečtením výrazů na pravých a levých stranách rovnic dostáváme
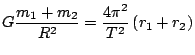 . Úpravou obdržíme
. Úpravou obdržíme
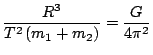 .
Na pravé straně rovnice je konstanta, tedy výraz na levé straně platí pro libovolnou soustavu dvou hmotných bodů, které se vzájemně přitahují podle zákona všeobecné gravitace a obíhají rovnoměrným pohybem po kruhových drahách kolem společného hmotného středu. Vztah platí i obecně, pro pohyb po eliptických drahách.
.
Na pravé straně rovnice je konstanta, tedy výraz na levé straně platí pro libovolnou soustavu dvou hmotných bodů, které se vzájemně přitahují podle zákona všeobecné gravitace a obíhají rovnoměrným pohybem po kruhových drahách kolem společného hmotného středu. Vztah platí i obecně, pro pohyb po eliptických drahách.
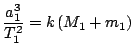 ,
,
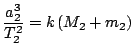 .
Podělením rovnic získáme používaný vztah pro přesný tvar III. Keplerova zákona
.
Podělením rovnic získáme používaný vztah pro přesný tvar III. Keplerova zákona
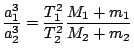 . Připomínáme,
že v uvedeném vztahu hmotnost centrálního tělesa je
. Připomínáme,
že v uvedeném vztahu hmotnost centrálního tělesa je 
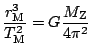 , odtud
, odtud
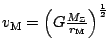 , tedy
, tedy
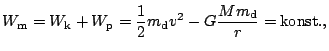
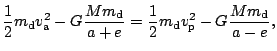
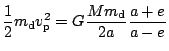 . Pro
mechanickou energii obdržíme
. Pro
mechanickou energii obdržíme
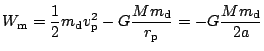 . Zobecněný vztah má
tvar
. Zobecněný vztah má
tvar
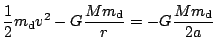 .
Odtud dostáváme důležitý vztah pro rychlost pohybu družice
.
Odtud dostáváme důležitý vztah pro rychlost pohybu družice
![$ \displaystyle
v=\left[GM\left(\frac{2}{r}-\frac{1}{a}\right)\right]^{\frac{1}{2}}$](img201.gif) . Rychlost družice při
dané vzdálenosti
. Rychlost družice při
dané vzdálenosti ![$ \displaystyle v_\mathrm{e}
=\left[GM\left(\frac{2}{r}-\frac{1}{a}\right)\right]^{\frac{1}{2}}$](img207.gif) .
.
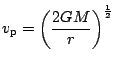 .
Položíme-li
.
Položíme-li
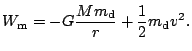
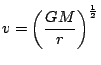 . Po dosazení do vztahu pro mechanickou
energii obdržíme
. Po dosazení do vztahu pro mechanickou
energii obdržíme
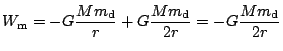 .
.
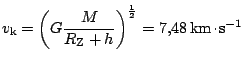 ,
dále
,
dále
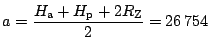 km. Rychlost na eliptické dráze je
km. Rychlost na eliptické dráze je
![$ \displaystyle v_\mathrm{p}
=\left[GM\left(\frac{2}{r}-\frac{1}{a}\right)\right]^{\frac{1}{2}}=
9,84\,\mathrm{km}\kern -1.2pt \cdot\kern -1.2pt \mathrm{s}^{-1}$](img219.gif) ,
,
![$ \displaystyle
T_\mathrm{p}=T_\mathrm{k}\left[\frac{2R_\mathrm{Z}+H_\mathrm{p}+...
...\left(R_\mathrm{Z}+H_\mathrm{p}\right)}\right]^{\frac{3}{2}}=12,1\,\mathrm{hod}$](img222.gif) .
.

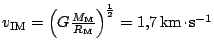 .
II. kosmická rychlost má hodnotu
.
II. kosmická rychlost má hodnotu
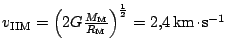 .
.

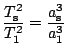 , což po dosazení dá
hodnotu
, což po dosazení dá
hodnotu
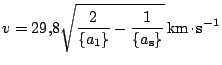 ,
vzdálenosti
,
vzdálenosti