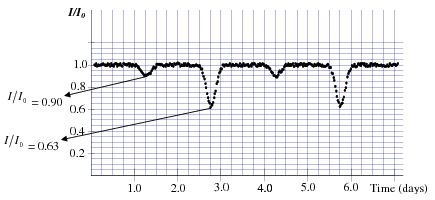
Úloha 9.20
Ve spektru dvojhvězdy byla pozorována absorpční
čára sodíku D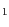 o laboratorní vlnové délce o laboratorní vlnové délce
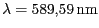 . V důsledku pohybu obou
hvězd a následného posuvu polohy této čáry byly
zjištěny údaje z tabulky: . V důsledku pohybu obou
hvězd a následného posuvu polohy této čáry byly
zjištěny údaje z tabulky:
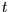 [den] [den] |
0,3 |
0,6 |
0,9 |
1,2 |
1,5 |
1,8 |
2,1 |
2,4 |
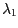 [nm] [nm] |
589,75 |
589,77 |
589,72 |
589,62 |
589,51 |
589,43 |
589,41 |
589,46 |
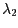 [nm] [nm] |
589,31 |
589,28 |
589,37 |
589,62 |
589,73 |
589,87 |
589,90 |
589,81 |
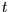 [den] [den] |
2,7 |
3,0 |
3,3 |
3,6 |
3,9 |
4,2 |
4,5 |
4,8 |
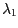 [nm] [nm] |
589,56 |
589,67 |
589,73 |
589,77 |
589,72 |
589,62 |
589,50 |
589,43 |
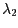 [nm] [nm] |
589,64 |
589,45 |
589,31 |
589,28 |
589,37 |
589,62 |
589,74 |
589,87 |
S využitím tabulky nalezněte oběžné
rychlosti 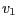 a a
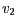 jednotlivých hvězd,
poměr hmotností jednotlivých hvězd,
poměr hmotností 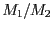 a hmotnost každé
hvězdy, vzdálenosti
a hmotnost každé
hvězdy, vzdálenosti 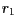 a a 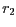 jednotlivých hvězd od
hmotného středu soustavy a vzdálenost
jednotlivých hvězd od
hmotného středu soustavy a vzdálenost 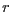 obou
hvězd. obou
hvězd.
|