Řešení úlohy 3.1
Pro I. kosmickou rychlost platí
Řešení úlohy 3.1
Pro
I. kosmickou rychlost platí
![]() ,
pro II. kosmickou rychlost
,
pro II. kosmickou rychlost
![]() . Parabolická rychlost vzhledem ke
Slunci je
. Parabolická rychlost vzhledem ke
Slunci je
![]() , střední rychlost Země
kolem Slunce
, střední rychlost Země
kolem Slunce
![]() , tedy potřebujeme
rychlost
, tedy potřebujeme
rychlost
![]() na hranici oblasti
přitažlivosti Země. Pro startovací rychlost ze Země
platí
na hranici oblasti
přitažlivosti Země. Pro startovací rychlost ze Země
platí
![]() .
.
Řešení úlohy 3.3
Pro rychlost na kruhové
dráze platí vztah
![]() ,
odtud určíme
,
odtud určíme
![]() .
.
Řešení úlohy 3.4
Nejprve stanovíme
![]() a
a
![]() , pro velikost
hlavní poloosy platí
, pro velikost
hlavní poloosy platí
![]() .
Rychlost v apogeu určíme ze vztahu
.
Rychlost v apogeu určíme ze vztahu
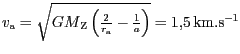 a v perigeu
a v perigeu
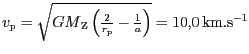 .
.
Řešení úlohy 3.5
Pro kruhovou dráhu
obdržíme
![]() .
Po zvýšení rychlosti se družice
dostane na eliptickou dráhu, pro velikost její hlavní poloosy
.
Po zvýšení rychlosti se družice
dostane na eliptickou dráhu, pro velikost její hlavní poloosy
![]() platí
platí
![]() , odtud
, odtud
![]() .
.
Řešení úlohy 3.6
Předpokládejme, že
změna rychlosti družice proběhne za velmi krátký
časový okamžik ve srovnání s velikostí oběžné
doby. Platí
![]() ,
dále ze vztahu
,
dále ze vztahu
![]() určíme
určíme
![]() .
Rychlost v perigeu eliptické dráhy je
.
Rychlost v perigeu eliptické dráhy je
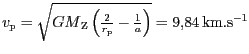 , změna
rychlosti
, změna
rychlosti
![]() .
Oběžnou dobu stanovíme z III. Keplerova zákona
.
Oběžnou dobu stanovíme z III. Keplerova zákona
![]() ,
kde
,
kde
![]() ,
,
![]() . Odtud při
. Odtud při
![]() .
.
![]() .
.
Řešení úlohy 3.7
Vykonaná práce při
přechodu z jedné na druhou oběžnou dráhu je rovna
![]() ,
pro rychlosti na kruhových oběžných drahách platí
,
pro rychlosti na kruhových oběžných drahách platí
![]() . Po dosazení
obdržíme
. Po dosazení
obdržíme
![]() .
.
Řešení úlohy 3.8
Minimální práce je rovna
![]() .
.
Řešení úlohy 3.9
Ze vztahu
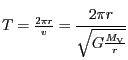 stanovíme
stanovíme
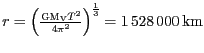 . Oblast aktivity Venuše vzhledem ke Slunci má
přibližný poloměr
. Oblast aktivity Venuše vzhledem ke Slunci má
přibližný poloměr
![]() , tudíž družice
bude velmi rychle zachycena gravitační silou Slunce.
, tudíž družice
bude velmi rychle zachycena gravitační silou Slunce.
Řešení úlohy 3.10
Platí
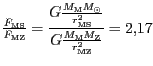 . Kolem Slunce obíhá barycentrum soustavy Země -
Měsíc.
. Kolem Slunce obíhá barycentrum soustavy Země -
Měsíc.
Řešení úlohy 3.11
Vztah pro slapovou sílu, kde Země je
rušené kosmické těleso a Měsíc respektive Slunce jsou
rušícími, je dán vztahem
![]() ,
kde
,
kde ![]() je vzdálenost středů obou uvažovaných
kosmických těles. Připomínáme, že vztah udává
převrácenou kubickou závislosti s mnohem rychlejším
poklesem síly. Po dosazení číselných hodnot obdržíme
pro velikost působících slapových sil Měsíce na Zemi
je vzdálenost středů obou uvažovaných
kosmických těles. Připomínáme, že vztah udává
převrácenou kubickou závislosti s mnohem rychlejším
poklesem síly. Po dosazení číselných hodnot obdržíme
pro velikost působících slapových sil Měsíce na Zemi
![]() a Slunce na Zemi
a Slunce na Zemi
![]() . Tedy prvně počítané slapové působení
činí 2/3 a druhé 1/3 z celkového slapového působení
obou kosmických těles. Slapové síly vyvolávané
Měsícem jsou přibližně 2,2krát větší
než slapové síly Slunce. Jinak vyjádřeno
slapové síly vytvářené Sluncem dosahují
přibližně pouze 46% slapových sil Měsíce. Při
hypotetickém zvětšení vzdálenosti Měsíce 2krát,
by jeho slapové působení pokleslo 8krát a stalo by se 4krát
slabší než slapové působení od Slunce.
. Tedy prvně počítané slapové působení
činí 2/3 a druhé 1/3 z celkového slapového působení
obou kosmických těles. Slapové síly vyvolávané
Měsícem jsou přibližně 2,2krát větší
než slapové síly Slunce. Jinak vyjádřeno
slapové síly vytvářené Sluncem dosahují
přibližně pouze 46% slapových sil Měsíce. Při
hypotetickém zvětšení vzdálenosti Měsíce 2krát,
by jeho slapové působení pokleslo 8krát a stalo by se 4krát
slabší než slapové působení od Slunce.
Řešení úlohy 3.12
V izolované soustavě, za
kterou můžeme zjednodušeně považovat soustavu
Země - Měsíc, platí zákon zachování momentu
hybnosti. Pro počáteční a koncový stav platí
![]() . Z platnosti podmínek
v zadání vyplývá
. Z platnosti podmínek
v zadání vyplývá
![]() +
+
![]() a
a
![]() . Moment
setrvačnosti Měsíce vzhledem k rotační ose Země je
. Moment
setrvačnosti Měsíce vzhledem k rotační ose Země je
![]() , jeho
současná dráhová úhlová rychlost
, jeho
současná dráhová úhlová rychlost
![]() . Dráhový moment hybnosti Měsíce
nyní
. Dráhový moment hybnosti Měsíce
nyní
![]() .
Počáteční
celkový moment hybnosti je
.
Počáteční
celkový moment hybnosti je
![]() . Aplikujeme zákon
zachování momentu hybnosti
. Aplikujeme zákon
zachování momentu hybnosti
![]() , kde
, kde
![]() .
Dále platí III. Keplerův zákon upravený do tvaru
.
Dále platí III. Keplerův zákon upravený do tvaru
![]() .
Po dosazení a úpravách obdržíme
.
Po dosazení a úpravách obdržíme
![]() . Rovněž z III. Keplerova zákona
získáme konečnou úhlovou rychlost
. Rovněž z III. Keplerova zákona
získáme konečnou úhlovou rychlost
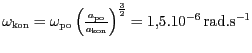 s konečnou oběžnou dobou
s konečnou oběžnou dobou
![]() dnů.
dnů.
Řešení úlohy 3.13
Použijeme III. Keplerův
zákon v přesném znění
![]() ,
kde hmotnost
,
kde hmotnost
![]() Měsíce zanedbáváme,
Měsíce zanedbáváme,
![]() je změněná hmotnost Země.
Úpravou vztahu obdržíme
je změněná hmotnost Země.
Úpravou vztahu obdržíme
![]()
![]()
![]() .
.
Řešení úlohy 3.14
Dosadíme do rovnice
vyjadřující, že dostředivé zrychlení je
vytvářeno silou přitažlivosti Slunce
![]() ,
kde
,
kde
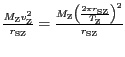 .
Obdobně v případě hypotetického přesunu na
dvojnásobnou vzdálenost platí
.
Obdobně v případě hypotetického přesunu na
dvojnásobnou vzdálenost platí
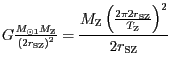 .
Podělením druhé rovnice první obdržíme po úpravě
.
Podělením druhé rovnice první obdržíme po úpravě
![]() .
.
Řešení úlohy 3.15
Dosadíme do rovnice
vyjadřující zákon zachování mechanické energie pro
pohyb Země
![]() .
Při zjednodušení na kruhovou dráhu dostáváme
.
Při zjednodušení na kruhovou dráhu dostáváme
![]()
![]()
![]() .
Následně dosadíme do rovnice pro zákon zachování
energie
.
Následně dosadíme do rovnice pro zákon zachování
energie
![]() .
Po úpravě obdržíme
.
Po úpravě obdržíme
![]() .
Podělením čitatelů
.
Podělením čitatelů
![]() , zvolíme
, zvolíme
![]() ,
,
![]() získáme vztah
získáme vztah
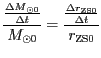
![]()
![]() . Přepočtením
získáme
. Přepočtením
získáme
![]() .
.
Řešení úlohy 3.16
Ke stanovení typu dráhy
určíme kruhovou a parabolickou rychlost v dané vzdálenosti
od Slunce,
![]() ,
,
![]() . Protože platí
. Protože platí
![]() , kometa se
pohybuje pro eliptické dráze. Ze vztahu pro rychlost komety
v perihéliu
, kometa se
pohybuje pro eliptické dráze. Ze vztahu pro rychlost komety
v perihéliu
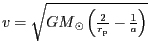 vyjádříme velikost velké poloosy
vyjádříme velikost velké poloosy
![]() .
Oběžnou dobu stanovíme z III. Keplerova zákona
.
Oběžnou dobu stanovíme z III. Keplerova zákona
![]() roků. Excentricitu vypočítáme
roků. Excentricitu vypočítáme
![]() .
Rychlost komety v aféliu je rovna
.
Rychlost komety v aféliu je rovna
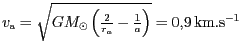 .
.
Řešení úlohy 3.17
Platí III. Keplerův zákon
![]() .
Při předpokládané oběžné době 2 roky
je velikost hlavní poloosy dráhy
.
Při předpokládané oběžné době 2 roky
je velikost hlavní poloosy dráhy
![]() .
Planetka s těmito parametry nemůže existovat.
.
Planetka s těmito parametry nemůže existovat.
Řešení úlohy 3.18
Pro rychlost v perihéliu
platí
![]() , pro rychlost v aféliu
, pro rychlost v aféliu
![]() . Pro kruhovou dráhu platí vztah
. Pro kruhovou dráhu platí vztah
![]() , kde rychlost je
, kde rychlost je
![]() a
a ![]() v AU. Dosazením
obdržíme
v AU. Dosazením
obdržíme
![]() .
.
Řešení úlohy 3.19
Za předpokladu ![]() platí
platí
![]() ,
kde
,
kde
![]() .
Oběžná doba kosmické lodi závisí na hustotě
planety.
.
Oběžná doba kosmické lodi závisí na hustotě
planety.
Řešení úlohy 3.20
Vyjdeme ze zákona
zachování energie
![]() a zákona zachování momentu hybnosti
a zákona zachování momentu hybnosti
![]() . Řešením
rovnic obdržíme vztah pro celkovou mechanickou energie
. Řešením
rovnic obdržíme vztah pro celkovou mechanickou energie
![]() ,
která závisí na velikosti velké poloosy.
,
která závisí na velikosti velké poloosy.
Řešení úlohy 3.21
Nejprve stanovíme velikost
kruhové rychlosti družice
![]() , po dosazení
obdržíme
, po dosazení
obdržíme
![]() .
Pro kinetickou energii obdržíme
.
Pro kinetickou energii obdržíme
![]() , pro potenciální energii
, pro potenciální energii
![]() . Připomínáme, že platí
viriálová věta
. Připomínáme, že platí
viriálová věta
![]() .
.
Řešení úlohy 3.22
Pro rychlost na kruhové
dráze platí
![]() . Pro rychlost v periseleniu platí
. Pro rychlost v periseleniu platí
![]() a pro rychlost v aposeleniu
a pro rychlost v aposeleniu
![]() .
.
Řešení úlohy 3.23
a) Při pohybu po kruhové
dráze kolem Měsíce platí
![]() ,
kde
,
kde
![]() . Po zapnutí
brzdícího motoru udílejícího kosmické lodi impuls, se
loď bude pohybovat po eliptické dráze s ohniskem ve
středu Měsíce. Při označení
. Po zapnutí
brzdícího motoru udílejícího kosmické lodi impuls, se
loď bude pohybovat po eliptické dráze s ohniskem ve
středu Měsíce. Při označení ![]() a
a
![]() rychlostí kosmické lodi v bodech
rychlostí kosmické lodi v bodech ![]() a
a ![]() zapíšeme
zákon zachování energie a momentu hybnosti
zapíšeme
zákon zachování energie a momentu hybnosti
![]() a
a
![]() .
Řešením posledně dvou uvedených rovnic nalezneme
.
Řešením posledně dvou uvedených rovnic nalezneme
![]() a po úpravě získáme
a po úpravě získáme
![]() . Změna
rychlosti
. Změna
rychlosti
![]() . Brzdící motor se zapíná
na krátkou dobu, proto můžeme zákon zachování hybnosti
soustavy kosmická loď - vyletující palivo zapsat ve tvaru
. Brzdící motor se zapíná
na krátkou dobu, proto můžeme zákon zachování hybnosti
soustavy kosmická loď - vyletující palivo zapsat ve tvaru
![]() .
Úpravou obdržíme
.
Úpravou obdržíme
![]() , odtud při
, odtud při
![]() platí
platí
![]() .
.
b) Vektor
![]() směřuje kolmo k vektoru
směřuje kolmo k vektoru
![]() , proto
, proto
![]() . Ze
zákona zachování mechanické energie dostaneme
. Ze
zákona zachování mechanické energie dostaneme
![]() a zákona zachování momentu hybnosti
a zákona zachování momentu hybnosti
![]() .
Řešením posledních dvou uvedených rovnic obdržíme
.
Řešením posledních dvou uvedených rovnic obdržíme
![]() . Při využití zákona
zachování hybnosti
. Při využití zákona
zachování hybnosti
![]() .
.
Řešení úlohy 3.24
Za předpokladu kruhových
drah planet můžeme jejich dráhový moment hybnosti zachytit
vztahem
![]() .
Při znalosti hmotností, poloměrů drah a
oběžných dob planet můžeme vypočítat
dráhové momenty hybnosti vybraných planet
.
Při znalosti hmotností, poloměrů drah a
oběžných dob planet můžeme vypočítat
dráhové momenty hybnosti vybraných planet
![]() ,
,
![]() ,
,
![]() ,
,
![]() . U Slunce je
rotační moment hybnosti
. U Slunce je
rotační moment hybnosti
![]() ,
činící
méně než zhruba 3 % celkového momentu hybnosti všech
planet, přestože jeho hmotnost je 99,9 % celkové hmotnosti
sluneční soustavy.
,
činící
méně než zhruba 3 % celkového momentu hybnosti všech
planet, přestože jeho hmotnost je 99,9 % celkové hmotnosti
sluneční soustavy.
Řešení úlohy 3.25
Úpravou III. Keplerova zákona
při zanedbání hmotnost Hyperiona
![]() ,
odtud
,
odtud
![]() .
.
Řešení úlohy 3.26
Platí
![]() ,
odtud
,
odtud
![]() . Za zvoleného předpokladu stejné hustoty obou těles a
s ohledem na poloměry respektive objemy těles obdržíme
. Za zvoleného předpokladu stejné hustoty obou těles a
s ohledem na poloměry respektive objemy těles obdržíme
![]() ,
,
![]() . Střední hustota je
rovna
. Střední hustota je
rovna
![]() .
.
Řešení úlohy 3.27
Rozdíl gravitačních
zrychlení ve středu Měsíce a na jeho
vzdálenějším okraji vyvolaných Zemí nacházející
se ve vzdálenosti
![]() je
roven
je
roven
![]() .
Pro určitou kritickou vzdálenost
.
Pro určitou kritickou vzdálenost
![]() Země - Měsíc bude
dostředivé zrychlení působící na povrch Měsíce
rovné odstředivému zrychlení
Země - Měsíc bude
dostředivé zrychlení působící na povrch Měsíce
rovné odstředivému zrychlení
![]() .
Po úpravě
.
Po úpravě
![]() a dosazení za hmotnosti obou těles obdržíme
a dosazení za hmotnosti obou těles obdržíme
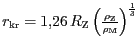 .
Kritická vzdálenost Měsíce je rovna 1,26 násobku
poloměru Země násobenému třetí odmocninou
z poměru hustot Země a Měsíce, což platí
v případě, že obě tělesa lze považovat za
tuhá. Po dosazení hodnot hustot
.
Kritická vzdálenost Měsíce je rovna 1,26 násobku
poloměru Země násobenému třetí odmocninou
z poměru hustot Země a Měsíce, což platí
v případě, že obě tělesa lze považovat za
tuhá. Po dosazení hodnot hustot
![]() a
a
![]() dostaneme
dostaneme
![]() .
V případě, že obě tělesa jsou kapalná je
násobným faktorem 2,4 a platí
.
V případě, že obě tělesa jsou kapalná je
násobným faktorem 2,4 a platí
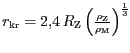 a tudíž
a tudíž
![]() .
.
Řešení úlohy 3.28
Nezbytná heliocentrická rychlost k dosažení Marsu má
hodnotu
![]() , Země se pohybuje po
dráze kolem Slunce se střední oběžnou rychlostí
, Země se pohybuje po
dráze kolem Slunce se střední oběžnou rychlostí
![]() ,
nutná rychlost kosmické sondy při
opouštění oblasti aktivity Země (sahající do
vzdálenosti přibližně 930000km) je dána rozdílem
obou rychlostí, tedy
,
nutná rychlost kosmické sondy při
opouštění oblasti aktivity Země (sahající do
vzdálenosti přibližně 930000km) je dána rozdílem
obou rychlostí, tedy
![]() . Minimální
počáteční tzv. startovací rychlost z povrchu Země je
určena vztahem
. Minimální
počáteční tzv. startovací rychlost z povrchu Země je
určena vztahem
![]() , kde
, kde
![]() je
hodnota druhé kosmické rychlosti. Přechod ze
Země
je
hodnota druhé kosmické rychlosti. Přechod ze
Země ![]() k Marsu
k Marsu ![]() se uskutečňuje po poloeliptické
přechodové dráze, velikost jejíž velké poloosy
se uskutečňuje po poloeliptické
přechodové dráze, velikost jejíž velké poloosy
![]() vypočítáme
vypočítáme
![]() v souladu s obrázkem.
Excentricitu
přechodové dráhy určíme ze vztahu
v souladu s obrázkem.
Excentricitu
přechodové dráhy určíme ze vztahu
![]() .
Dobu letu získáme z III. Keplerova zákona
.
Dobu letu získáme z III. Keplerova zákona
![]() ,
odkud po dosazení obdržíme hodnotu
,
odkud po dosazení obdržíme hodnotu
![]() .
.
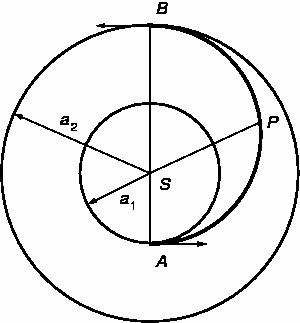
Je vhodné, aby se v okamžiku startu nacházela Země v
perihéliu své dráhy, kde je rychlost planety asi o
![]() vyšší než v aféliu a má
hodnotu
vyšší než v aféliu a má
hodnotu
![]() . Vyšší startovací
rychlost umožňuje zkrácení dráhy letu a také
výhodnější kratší rádiové spojení
s případnými přistávacími moduly v okamžiku
přiblížení a přistání kosmických lodí,
neboť Mars je v menší vzdálenosti od Země. Kosmické
sondy nesoucí na palubě Mars Pathfinder se pohybovaly po
přechodových drahách blížících se hohmannovským.
. Vyšší startovací
rychlost umožňuje zkrácení dráhy letu a také
výhodnější kratší rádiové spojení
s případnými přistávacími moduly v okamžiku
přiblížení a přistání kosmických lodí,
neboť Mars je v menší vzdálenosti od Země. Kosmické
sondy nesoucí na palubě Mars Pathfinder se pohybovaly po
přechodových drahách blížících se hohmannovským.