Řešení úlohy 12.1
Zvolíme molekulární hmotnost
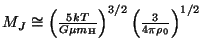 . Po
dosazení obdržíme
. Po
dosazení obdržíme
Řešení úlohy 12.1
Zvolíme molekulární hmotnost ![]() a dosadíme do vztahu
a dosadíme do vztahu
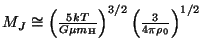 . Po
dosazení obdržíme
. Po
dosazení obdržíme
![]() .
.
Řešení úlohy 12.3
Dosadíme do vztahu pro dobu volného pádu
![]() .
.
Řešení úlohy 12.4
Při smršťování je polovina uvolněné gravitační potenciální energie
vyzářena
![]() .
Velikost vyzářené energie určíme ze vztahu vyjádřeném v absolutních hodnotách
.
Velikost vyzářené energie určíme ze vztahu vyjádřeném v absolutních hodnotách
![]() . Střední hodnota zářivého výkonu protohvězdy je
. Střední hodnota zářivého výkonu protohvězdy je
![]() vyz
vyz![]() W
W![]() .
.
Řešení úlohy 12.5
Pro střední dobu platí
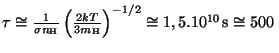 roků.
roků.
Řešení úlohy 12.6
Dosazením obdržíme
![]() .
.
Řešení úlohy 12.7
Doba pobytu je
![]() roků při uvedených podmínkách.
roků při uvedených podmínkách.
Řešení úlohy 12.8
Dosadíme do uvedených vztahů a vytvoříme tabulku. Tepelná rychlost atomů vodíku je o řád vyšší, než úniková rychlost atomů na okraji mračna, které drží pohromadě vlastní expanzí nikoliv gravitací.
| Mlhovina | Průměr | Hmotnost |
|
|
|
| [pc] | [ |
[
|
[K] | [
|
|
| M 8 | |||||
| M 17 |
Řešení úlohy 12.9
Vyjdeme ze vztahu
![]() . Při zvětšení vzdálenosti
. Při zvětšení vzdálenosti
![]() se zvětší pozorovaná hvězdná velikost o
se zvětší pozorovaná hvězdná velikost o ![]() mag, tedy poloha hvězdy
se posune směrem dolů. V případě mezihvězdného mračna prachu se zvětší
pozorovaná hvězdná velikost rovněž o
mag, tedy poloha hvězdy
se posune směrem dolů. V případě mezihvězdného mračna prachu se zvětší
pozorovaná hvězdná velikost rovněž o ![]() mag, tudíž poloha hvězdy se posune dolů
na H - R diagramu.
mag, tudíž poloha hvězdy se posune dolů
na H - R diagramu.
Řešení úlohy 12.10
Dosazením do Stefanova-Boltzmannova zákona určíme zářivý výkon
hvězdy
![]() . Za podmínek zadání přibližně platí
. Za podmínek zadání přibližně platí
![]() , odkud
, odkud
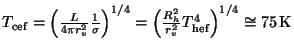 .
.
Řešení úlohy 12.11
Při tak vysoké povrchové teplotě hvězdy připadá velká část záření na
lymanovské kontinuum
![]() nm, které je absorbováno mlhovinou a ionizuje přitom vodík. Ve viditelném oboru spektra je mlhovina průzračná pro záření jak centrální hvězdy tak i objektů umístěných v radiálním směru za ní.
nm, které je absorbováno mlhovinou a ionizuje přitom vodík. Ve viditelném oboru spektra je mlhovina průzračná pro záření jak centrální hvězdy tak i objektů umístěných v radiálním směru za ní.
Řešení úlohy 12.12
Geometrická délka zorného paprsku je
![$ l=2\left\{\left[r^2-x^2\right]^{1/2}-\left[\left(r-d\right)^2-x^2\right]^{1/2}\right\}$](img1538.gif) , kde
, kde ![]() je vzdálenost záměrného paprsku do středu mlhoviny. Při zadaných podmínkách bude mlhovina vypadat jako planetární.
je vzdálenost záměrného paprsku do středu mlhoviny. Při zadaných podmínkách bude mlhovina vypadat jako planetární.
Řešení úlohy 12.13
Při zadané povrchové teplotě a poloměru je zářivý výkon hvězdy
![]() , tedy
, tedy
![]() . Z Wienova posunovacího zákona
obdržíme
. Z Wienova posunovacího zákona
obdržíme
![]() , což je
podstatně méně než
, což je
podstatně méně než ![]() nm nezbytných pro ionizaci vodíku za základního
stavu. Většina fotonů je schopna vyvolat ionizaci, pro zjednodušení
předpokládejme, že všechny emitované fotony mají
nm nezbytných pro ionizaci vodíku za základního
stavu. Většina fotonů je schopna vyvolat ionizaci, pro zjednodušení
předpokládejme, že všechny emitované fotony mají ![]() stejné. Jejich
střední energie je
stejné. Jejich
střední energie je
![]() J. Celkový počet
fotonů je
J. Celkový počet
fotonů je
![]() . Počet fotonů vyzařovaných
z
. Počet fotonů vyzařovaných
z
![]() za 1 sekundu lze vyjádřit
za 1 sekundu lze vyjádřit
![]() . Při zadaných povrchových teplotách téměř
každý foton může ionizovat atom, tedy počet ionizací je roven počtu fotonů
vyzařovaných za 1 sekundu. Celkový počet fotonů vyzařovaných hvězdou je
. Při zadaných povrchových teplotách téměř
každý foton může ionizovat atom, tedy počet ionizací je roven počtu fotonů
vyzařovaných za 1 sekundu. Celkový počet fotonů vyzařovaných hvězdou je
![]() , což odpovídá výsledkům
získávaným jinými způsoby. Jestliže dojde ke zvýšení teploty na
, což odpovídá výsledkům
získávaným jinými způsoby. Jestliže dojde ke zvýšení teploty na
![]() , tedy na dvojnásobek, počet fotonů se zvýší osminásobně.
, tedy na dvojnásobek, počet fotonů se zvýší osminásobně.
Řešení úlohy 12.14
Podle Wienova posunovacího zákona
![]() nm, tedy
existují podmínky pro ionizaci vodíku ze základního stavu. Nezbytná energii je
rovna
nm, tedy
existují podmínky pro ionizaci vodíku ze základního stavu. Nezbytná energii je
rovna
![]() J. Při zjednodušujících
předpokladech, že všechny
emitované fotony mají stejnou vlnovou délku, je celkový počet fotonů produkovaných
hvězdou za sekundu
J. Při zjednodušujících
předpokladech, že všechny
emitované fotony mají stejnou vlnovou délku, je celkový počet fotonů produkovaných
hvězdou za sekundu
![]() . Při znalosti
rekombinačního koeficientu
. Při znalosti
rekombinačního koeficientu
![]() a hodnotě hustoty mračna
vodíku
a hodnotě hustoty mračna
vodíku
![]() dostaneme dosazením pro poloměr Strömgrenovy oblasti
dostaneme dosazením pro poloměr Strömgrenovy oblasti
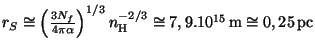 .
.
Řešení úlohy 12.15
Velikost H II oblasti je určována poloměrem a teplotou ionizující
hvězdy a hustotou látky v Strömgrenově oblasti. Platí vztah
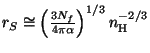 .
.
Řešení úlohy 12.16
Základní složkou mezihvězdné látky je vodík, který je v oblastech H II prakticky plně ionizován. V stacionárním stavu počet ionizací je roven počtu
rekombinací, které probíhají při srážkách protonů a elektronů. Jejich počet
v objemové jednotce je proto
![]() nebo
nebo ![]() ,
,
![]() . Celkový počet rekombinací v oblasti H II je
. Celkový počet rekombinací v oblasti H II je
![]() , kde
, kde ![]() je poloměr oblasti H II. Z druhé
strany počet rekombinací je roven počtu ionizací, které jsou určeny parametry
vyzařující hvězdy. Shrnuto z výše uvedeného platí
je poloměr oblasti H II. Z druhé
strany počet rekombinací je roven počtu ionizací, které jsou určeny parametry
vyzařující hvězdy. Shrnuto z výše uvedeného platí
![]() .
.
Pro číselnou představu uvádíme tabulku poloměrů oblastí vodíku H II u hvězd
hlavní posloupnosti různých spektrálních tříd při
![]() .
.
| Spektrální třída | Spektrální třída | ||
| O5 | 140 | B1 | 17 |
| O6 | 110 | B2 | 11 |
| O7 | 87 | B3 | 7,2 |
| O8 | 66 | B4 | 5,2 |
| O9 | 46 | B5 | 3,7 |
| B0 | 26 | A0 | 0,5 |
Řešení úlohy 12.17
Nejprve určíme počet kvant záření - fotonů uvolňovaných z
![]() povrchu hvězdy za
povrchu hvězdy za ![]() s,
s,
![]() , kde
, kde
![]() . Dosazením obdržíme počet
kvant lymanovského kontinua
. Dosazením obdržíme počet
kvant lymanovského kontinua
![]() fotonů.m
fotonů.m![]() s
s![]() . Při
poloměru hvězdy
. Při
poloměru hvězdy
![]() dostaneme celkový počet fotonů uvolňovaných
hvězdou
dostaneme celkový počet fotonů uvolňovaných
hvězdou
![]() fotonů.s
fotonů.s![]() . Poloměr Strömgrenovy
oblasti určíme
. Poloměr Strömgrenovy
oblasti určíme
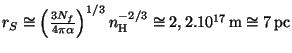 .
.
Řešení úlohy 12.18
Ionizovat vodík je schopné záření s vlnovou délkou
![]() nm, tedy s frekvencí
nm, tedy s frekvencí ![]() , kde
, kde
![]() . Hledaná část energie záření je
. Hledaná část energie záření je
![]() ,
kde
,
kde
![]() .
Pro vodík
.
Pro vodík
![]() , při
, při
![]()
![]() , tudíž
, tudíž
![]() . Při
. Při ![]() platí
platí
![]() . Dále
. Dále
![]() . Celkově
. Celkově
![]() připadá na ionizaci vodíku,
hvězda má příliš nízkou teplotu pro výraznější ionizaci.
připadá na ionizaci vodíku,
hvězda má příliš nízkou teplotu pro výraznější ionizaci.
Řešení úlohy 12.19
Stupeň excitace atomů vyjadřujeme z Boltzmannovy rovnice
![]() , kde
, kde
![]() , při
, při
![]() . Boltzmannova
rovnice má tvar
. Boltzmannova
rovnice má tvar
![]() . Kinetická teplota
mezihvězdného vodíku je vždy větší než
. Kinetická teplota
mezihvězdného vodíku je vždy větší než ![]() K, tedy
K, tedy
![]()
![]() , poměr
, poměr
![]() se nepatrně mění s teplotou mezihvězdného plynu. Ve vyšším stavu s antiparalelním spinem (přesněji v důsledku rozdílnosti orientací magnetických momentů protonu a elektronu) se bude nacházet 75% atomů vodíku.
se nepatrně mění s teplotou mezihvězdného plynu. Ve vyšším stavu s antiparalelním spinem (přesněji v důsledku rozdílnosti orientací magnetických momentů protonu a elektronu) se bude nacházet 75% atomů vodíku.
Řešení úlohy 12.20
Dosadíme do vztahu
![]() pro
pro
![]() K
a
K
a
![]() K. Obdržíme
K. Obdržíme
![]() při
při
![]() K,
K,
![]() při
při
![]() K.
K.
Řešení úlohy 12.21
Podle uvedeného vztahu spektrální čáry H![]() , H
, H![]() budou
zeslabeny v mezihvězdném prostředí absorpcí závislou na vlnové délce, tedy
rozdílně pro obě čáry. Proto poměr naměřených zářivých toků v uvedených čarách
je odlišný od teoretické hodnoty, závisí na vzdálenosti. Hodnoty absorpce
budou
zeslabeny v mezihvězdném prostředí absorpcí závislou na vlnové délce, tedy
rozdílně pro obě čáry. Proto poměr naměřených zářivých toků v uvedených čarách
je odlišný od teoretické hodnoty, závisí na vzdálenosti. Hodnoty absorpce
![]() v magnitudách a zeslabení v čarách H
v magnitudách a zeslabení v čarách H![]() a H
a H![]() jsou:
jsou:
![]() zeslabení
zeslabení
![]() ,
,
![]() zeslabení
zeslabení
![]() .
Pro pozorovaný a teoretický poměr intenzit spektrálních čar H
.
Pro pozorovaný a teoretický poměr intenzit spektrálních čar H![]() a
H
a
H![]() platí:
platí:
![]() .
Obdržíme vztah mezi pozorovaným a teoretickým Balmerovým dekrementem a
vzdáleností. Dosazením číselných hodnot obdržíme
.
Obdržíme vztah mezi pozorovaným a teoretickým Balmerovým dekrementem a
vzdáleností. Dosazením číselných hodnot obdržíme
![]() .
.
Řešení úlohy 12.22
Ze zadání úlohy dostaneme
![]() . Hmotnost elektronů v mlhovině
odhadneme
. Hmotnost elektronů v mlhovině
odhadneme
![]() .
Tento odhad se zvýší na
.
Tento odhad se zvýší na
![]() kg při započtení hmotnosti protonů a dále atomů helia, kterých je v mlhovině přibližně 16% počtu atomů vodíku a započtením hmotnosti i těžších prvků.
kg při započtení hmotnosti protonů a dále atomů helia, kterých je v mlhovině přibližně 16% počtu atomů vodíku a započtením hmotnosti i těžších prvků.
Řešení úlohy 12.23
![]() m,
m,
![]() m. Rozšíření srážkami je vzhledem k nízké teplotě a malé hustotě velmi malé.
m. Rozšíření srážkami je vzhledem k nízké teplotě a malé hustotě velmi malé.
Řešení úlohy 12.24
Využijeme vztah
![]() pro šířky
obou čar, řešíme dvě rovnice, obdržíme kinetickou teplotu
pro šířky
obou čar, řešíme dvě rovnice, obdržíme kinetickou teplotu
![]() a
a
![]() .
.
Řešení úlohy 12.25
Vlnová délka fotonu vyzařovaného při přechodu z energetické hladiny ![]() na
na ![]() je dána vztahem
je dána vztahem
![]() , kde
, kde
![]() . Položíme
. Položíme ![]() a předpokládáme, že
a předpokládáme, že ![]() .
Dosazením obdržíme
.
Dosazením obdržíme
![]() . Podle
tohoto vztahu spektrální čára H
. Podle
tohoto vztahu spektrální čára H
![]() má vlnovou délku
přibližně
má vlnovou délku
přibližně
![]() .
.
Řešení úlohy 12.26
Řešení: Vyjdeme ze vztahu pro frekvenci fotonu vyzařovaného při přechodu atomu
vodíku z energetické hladiny ![]() na
na ![]()
![]() , kde
, kde
![]() . Položíme
. Položíme
![]() a předpokládáme, že
a předpokládáme, že
![]() a
a
![]() . Obdržíme
. Obdržíme
![]() . Odtud je zřejmé, že při zvětšení
. Odtud je zřejmé, že při zvětšení ![]() o
jednotku narůstá frekvence odpovídajícího přechodu o stejnou velikost
o
jednotku narůstá frekvence odpovídajícího přechodu o stejnou velikost
![]() , která
je frekvencí čáry H
, která
je frekvencí čáry H![]() .
.
Řešení úlohy 12.27
Pro objem mlhoviny platí
![]() , pro zářivý
výkon platí
, pro zářivý
výkon platí
![]() . Úpravou dostaneme
. Úpravou dostaneme
![]() .
.
Řešení úlohy 12.28
Při průchodu záření přes mračno plynu se zeslabuje ![]() krát,
kde
krát,
kde ![]() je optická tloušťka vrstvy plynu. Ve středu čáry L
je optická tloušťka vrstvy plynu. Ve středu čáry L![]() je rovna
je rovna
![]() , kde
, kde ![]() je celkový počet atomů vodíku podél procházejícího se
paprsku. Absorpce se stává podstatnou, jestliže
je celkový počet atomů vodíku podél procházejícího se
paprsku. Absorpce se stává podstatnou, jestliže
![]() . Odpovídající
hustota na paprsku je
. Odpovídající
hustota na paprsku je
![]() . Spektrální analýza je tudíž velmi citlivou metodou.
. Spektrální analýza je tudíž velmi citlivou metodou.
Řešení úlohy 12.29
Ze vztahu
![]() určíme
určíme
![]() .
.
Řešení úlohy 12.30
Platí ![]() , odtud pro poloměr
, odtud pro poloměr ![]() v pc dostaneme
v pc dostaneme
![]() , je-li
, je-li ![]() v [GeV] a
v [GeV] a ![]() [T]. Dosazením obdržíme
[T]. Dosazením obdržíme
![]() .
.