Řešení úlohy 13.1
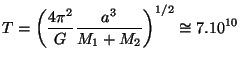 roků,
tedy asi 70 miliard let. Tato doba převyšuje stáří vesmíru, jde o teoretický
výpočet.
roků,
tedy asi 70 miliard let. Tato doba převyšuje stáří vesmíru, jde o teoretický
výpočet.
Řešení úlohy 13.1
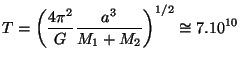 roků,
tedy asi 70 miliard let. Tato doba převyšuje stáří vesmíru, jde o teoretický
výpočet.
roků,
tedy asi 70 miliard let. Tato doba převyšuje stáří vesmíru, jde o teoretický
výpočet.
Řešení úlohy 13.2
Dosazením obdržíme
![]()
Řešení úlohy 13.3
Při výběru vhodných čar vyjdeme ze vztahu
![]() , kde
, kde ![]() musí být v optické části
spektra. Tedy v případě a) všechny čáry od Ne III, b) čáry C III až po čáru Ne
III, c) čáry L
musí být v optické části
spektra. Tedy v případě a) všechny čáry od Ne III, b) čáry C III až po čáru Ne
III, c) čáry L![]() až C IV.
až C IV.
Řešení úlohy 13.4
Využijeme vztah
![]() . Nejvhodnější a
nejčastěji používanou čarou je L
. Nejvhodnější a
nejčastěji používanou čarou je L![]() .
.
Řešení úlohy 13.5
Použitím vztahu
![]() l
l![]() p zjistíme, že jde
postupně o čáry H
p zjistíme, že jde
postupně o čáry H![]() , H
, H![]() , H
, H![]() vodíku. Vzdálenost je
vodíku. Vzdálenost je
![]() Mpc. Zářivý výkon kvasaru stanovíme ze vztahu
Mpc. Zářivý výkon kvasaru stanovíme ze vztahu
![]() bol
bol![]() W.
W.
Řešení úlohy 13.6
Vzdálenost kvasaru určíme ze vztahu
![]() Mpc.
Přibližný skutečný průměr kvasaru je
Mpc.
Přibližný skutečný průměr kvasaru je
![]() . Velikost výtrysku je
. Velikost výtrysku je
![]() . Zářivý výkon kvasaru je
. Zářivý výkon kvasaru je
![]() .
.
Řešení úlohy 13.7
Úbytek hmoty je roven
![]() . Při termonukleárním
hoření je úbytek přibližně
. Při termonukleárním
hoření je úbytek přibližně
![]() , při akreci a volbě
, při akreci a volbě
![]() obdržíme
obdržíme
![]() .
.
Řešení úlohy 13.8
U první cefeidy
![]() mag,
mag,
![]() dne. Ze závislosti
dne. Ze závislosti
![]() stanovíme
stanovíme
![]() mag. Dosazením do vztahu
mag. Dosazením do vztahu
![]() ,
,
![]() Mpc. U druhé cefeidy analogicky
Mpc. U druhé cefeidy analogicky
![]() mag,
mag,
![]() dne,
dne,
![]() mag. Vzdálenost
mag. Vzdálenost
![]() pc, tudíž
pc, tudíž
![]() Mpc.
Mpc.
Řešení úlohy 13.9
Hmotnost centrálního tělesa - černé díry určíme z III. Keplerova zákona
v přesném tvaru
![]() .
.
Řešení úlohy 13.10
Podle Hubbleova zákona
![]() Mpc. Předpokládejte, že
Velká zeď je tvořena gigantickou kupou galaxií, pro kterou platí viriálová věta.
Po dosazení údajů naší Galaxie obdržíme pro hmotnost kupy galaxií
Mpc. Předpokládejte, že
Velká zeď je tvořena gigantickou kupou galaxií, pro kterou platí viriálová věta.
Po dosazení údajů naší Galaxie obdržíme pro hmotnost kupy galaxií
![]() kg
kg![]() .
.
Řešení úlohy 13.11
Rychlost vzdalování je
![]() , vzdálenost
, vzdálenost
![]() Mpc.
Mpc.
Řešení úlohy 13.12
Vyjdeme ze vztahu pro Eddingtonův zářivý výkon
![]() Ed
Ed![]() p
p![]() T. Při 5% účinnosti je zářivý výkon aktivního
galaktického jádra
T. Při 5% účinnosti je zářivý výkon aktivního
galaktického jádra
![]() W.
W.
Řešení úlohy 13.13
Schwarzschildův poloměr černé díry je
![]() . Předpokládáme tempo pádu látky
o hmotnosti
. Předpokládáme tempo pádu látky
o hmotnosti
![]() .
Uvolněná gravitační potenciální energie je
.
Uvolněná gravitační potenciální energie je
![]() , což pro
zářivý výkon aktivní galaxie dává
, což pro
zářivý výkon aktivní galaxie dává
![]() .
.
Řešení úlohy 13.14
V důsledku pohybu mračen dochází k rozšíření čáry. Platí vztah pro
Dopplerův jev
![]() . Polovina pozorované šířky
. Polovina pozorované šířky
![]() nm odpovídá maximálnímu posuvu čar do červené respektive fialové části
optického spektra pro mračna pohybující se největší rychlostí podél zorného
paprsku. Pro vlnovou délku
nm odpovídá maximálnímu posuvu čar do červené respektive fialové části
optického spektra pro mračna pohybující se největší rychlostí podél zorného
paprsku. Pro vlnovou délku
![]() nm obdržíme při dosazení
nm obdržíme při dosazení
![]() .
.
Řešení úlohy 13.15
Nejprve z Hubbleova zákona stanovíme vzdálenost
![]() .
Úhlový poloměr převedeme,
.
Úhlový poloměr převedeme,
![]() rad. Skutečný poloměr prstence je
rad. Skutečný poloměr prstence je
![]() m. Při zanedbání hmotnosti látky vně disku a jejím
sféricko-symetrickém rozložení můžeme psát
m. Při zanedbání hmotnosti látky vně disku a jejím
sféricko-symetrickém rozložení můžeme psát
![]() . Dosazením do vztahu pro
Schwarzschildův poloměr dostaneme
. Dosazením do vztahu pro
Schwarzschildův poloměr dostaneme
![]() pc.
pc.
Řešení úlohy 13.16
Z Hubbleova zákona stanovíme vzdálenost
![]() . Při známé úhlové
velikosti poloměru
. Při známé úhlové
velikosti poloměru
![]() rad obdržíme pro skutečný poloměr
rad obdržíme pro skutečný poloměr
![]() pc. Hmotnost určíme ze vztahu
pc. Hmotnost určíme ze vztahu
![]() .
.
Řešení úlohy 13.17
Rychlost vzdalování stanovíme ze vztahu
![]() . Vzdálenost určíme z Hubbleova
zákona
. Vzdálenost určíme z Hubbleova
zákona
![]() . Skutečná lineární velikost zdroje je
. Skutečná lineární velikost zdroje je
![]() .
.
Řešení úlohy 13.18
Rádiový výkon galaxie vypočteme
![]() .
.
Řešení úlohy 13.19
Při hodnotě
![]() je
rychlost
je
rychlost
![]() .
.
Řešení úlohy 13.20
Nejprve určíme vzdálenost
![]() Mpc. Zářivý
výkon v rádiovém oboru je
Mpc. Zářivý
výkon v rádiovém oboru je
![]() .
.
Řešení úlohy 13.21
Při
![]() . Rychlost tepelného pohybu při zadané teplotě je
. Rychlost tepelného pohybu při zadané teplotě je
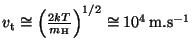 , kde
předpokládáme hmotnost atomu vodíku
, kde
předpokládáme hmotnost atomu vodíku
![]() kg. Tudíž vznik spektrálních čar
v kvasarech bude spojen s pohybem celých oblastí - mračen vyzařujícího plynu, jejich rychlost podstatně převyšuje rychlost tepelného pohybu částic.
kg. Tudíž vznik spektrálních čar
v kvasarech bude spojen s pohybem celých oblastí - mračen vyzařujícího plynu, jejich rychlost podstatně převyšuje rychlost tepelného pohybu částic.
Řešení úlohy 13.22
Minimální hmotnost černé díry je
![]() , minimální doba
proměnnosti je
, minimální doba
proměnnosti je ![]() hod.
hod.
Řešení úlohy 13.24
Pro gravitačně vázanou kupu platí viriálová věta
![]() , dosazením obdržíme
, dosazením obdržíme
![]() , odkud
, odkud
![]() .
.
Řešení úlohy 13.25
Pro teplotu záření ve směru apexu platí
![]() ,
,
![]() . Dosazením
určíme
. Dosazením
určíme
![]() .
.
Řešení úlohy 13.26
Z upravené Pogsonovy rovnice, při zadaných podmínkách, dostaneme pro vzdálenost
vztah
![]() . Celkový počet galaxií s hvězdnou velikostí
. Celkový počet galaxií s hvězdnou velikostí ![]() je roven
je roven
![]() . Odtud pro
poměr dostaneme
. Odtud pro
poměr dostaneme
![]() .
.
Řešení úlohy 13.27
Celkový počet fotonů v
![]() je
je
![]() .
V každém m
.
V každém m![]() je v současné době
je v současné době
![]() fotonů.
Předpokládáme-li, že základní příspěvek pro střední hustotu vesmíru dává vodík,
potom počet protonů je roven
fotonů.
Předpokládáme-li, že základní příspěvek pro střední hustotu vesmíru dává vodík,
potom počet protonů je roven
![]() . Při započtení části skryté
hmoty, kterou by mohla tvořit např. neutrina s nenulovou klidovou hmotností, by
koncentrace protonů byla ještě nižší. Shrnuto ve vesmíru je reliktních fotonů
asi
. Při započtení části skryté
hmoty, kterou by mohla tvořit např. neutrina s nenulovou klidovou hmotností, by
koncentrace protonů byla ještě nižší. Shrnuto ve vesmíru je reliktních fotonů
asi ![]() krát více než protonů. Základní jednotky stavební hierarchie
vesmíru - hvězdy však jsou složeny převážně z protonů.
krát více než protonů. Základní jednotky stavební hierarchie
vesmíru - hvězdy však jsou složeny převážně z protonů.
Řešení úlohy 13.28
Zkoumejme sférickou oblast prostoru o hmotnosti
![]() ,
,
![]() ,
, ![]() . V ní se pohybují částice
- galaxie o hmotnosti
. V ní se pohybují částice
- galaxie o hmotnosti ![]() , částice na povrchu koule má rychlost
, částice na povrchu koule má rychlost ![]() . Platí
vztah pro celkovou mechanickou energii
. Platí
vztah pro celkovou mechanickou energii
![]() .
Odtud pro hustotu energie
.
Odtud pro hustotu energie ![]() dostaneme
dostaneme
![]() .
V určitém čase
.
V určitém čase ![]() , platí podle Hubbleova zákona
, platí podle Hubbleova zákona
![]() a dále
a dále
![]() . Úpravou obdržíme
. Úpravou obdržíme
![]() . V kritickém stavu při
. V kritickém stavu při
![]() je
je
![]() platí
platí
![]() , odtud
, odtud
![]() . Při střední rychlosti expanze
. Při střední rychlosti expanze
![]() , odkud s použitím Hubbleova zákona
, odkud s použitím Hubbleova zákona ![]() obdržíme
obdržíme
![]() . Přijmeme-li Hubbleovu konstantu
. Přijmeme-li Hubbleovu konstantu
![]() je
je
![]() roků.
roků.