Počítačové úlohy - řešení

Řešení úlohy 14.1
Na stránce http://simbad.u-strasbg.fr/simbad/ zvolíme hledání prostřednictvím názvu ("Query by identifier") a jako "Identifier" zadáme název hvězdy.
a) $\alpha=14^\mathrm{h} 15^\mathrm{m} 39,6720^{s}$, $\delta=19^\circ 10' 56,677''$, $v_\mathrm{rad}=-5,2\pm 0,9\,\mathrm{km}.\mathrm{s}^{-1}$, $\pi=(88,85\pm0,74).10^{-3}\,\mathrm{arcsec}$, b) $\alpha=5^\mathrm{h}40^\mathrm{m}56,3704^{s}$, $\delta= -1^\circ30' 25,852''$, $v_\mathrm{rad}=27\pm5\,\mathrm{km}.\mathrm{s}^{-1}$, $\pi=(1,96\pm0,98).10^{-3}\,\mathrm{arcsec}$, c) $\alpha=0^\mathrm{h}42^\mathrm{m}44,31^{s}$, $\delta= 41^\circ 16' 09,4''$, $v_\mathrm{rad}=-301\pm7\,\mathrm{km}.\mathrm{s}^{-1}$.

Řešení úlohy 14.2
Na stránce http://adsabs.harvard.edu zvolíme "Search", "Astronomy and Astrophysics Search", hledáme např. články autora "Asplund" z roku 2005. Vybereme hledaný článek, který je možné získat prostřednictvím stránek xxx.lanl.gov (volba "arXiv e-print"). V Tabulce 1 tohoto článku jsou uvedeny hodnoty relativního zastoupení jednotlivých prvků jako $\log(N_\mathrm{prvek}/N_\mathrm{H})+12$. S jejich pomocí nakreslíme graf a spočteme relativní hmotnostní zastoupení těžších prvků $Z=0,0122$.

Řešení úlohy 14.3
Na stránkách CDS (http://cds.u-strasbg.fr) zvolíme VizieR, databáze "HIP" (Hipparcos), klepneme na "Find Catalogue", zvolíme "I/239/hip_main", v políčku Vmag vyplníme "<6", zvolíme "Sort" podle políčka "Plx", zvolíme "Output Order" jako "-" a klepneme na "Submit Query" a získáme seznam nejbližších a nejjasnějších hvězd (viz tabulka, ve které je zaneseno prvních deset z nich). Označení bylo získáno pomocí databáze SIMBAD.

HIP	hvězda	$m_\mathrm{V}$ [mag]	$\pi$ [ $10^{-3}\,\mathrm{arcec}$]
71681	$\alpha$ Cen B	1,35	$742,12 \pm 1,40$
71683	$\alpha$ Cen A	-0,01	$742,12 \pm 1,40$
32349	$\alpha$ CMa (Sirius)	-1,44	$379,21 \pm 1,58$
16537	$\varepsilon$ Eri	3,72	$310,75 \pm 0,85$
104214	61 Cyg	5,20	$287,13 \pm 1,51$
37279	$\alpha$ CMi (Prokyon)	0,40	$285,93 \pm 0,88$
108870	$\varepsilon$ Ind	4,69	$275,76 \pm 0,69$
8102	$\tau$ Cet	3,49	$274,17 \pm 0,80$
19849	$o$ Eri	4,43	$198,24 \pm 0,84$
88601	70 Oph	4,03	$196,62 \pm 1,38$

Řešení úlohy 14.4
Na stránce http://adsabs.harvard.edu zvolíme vyhledávání ("Search"), "Astronomy and Astrophysics Search" a jako položku "Title Words" zvolíme klíčová slova "Halley comet splitting". Získáme několik odkazů věnujících se rozpadu jádra Halleyovy komety během jejího posledního průchodu kolem Slunce. Tvrzení je jednou z úspěšných předpovědí autora.

Řešení úlohy 14.5
Pro spektrální hustotu energie vyzařování černého tělesa platí

$$E(\lambda)=\frac{8\pi c h}{\lambda^5}\frac{1}{{\mathrm e}^{hc/\lambda k T}-1}.$$

Pro výpočet lze použít například následující funkci:

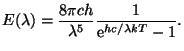
function b(tep,lam:double):double;

const h=6.6256e-34;     {Planckova konstanta}
      c=2.99792e8;      {rychlost svetla}
      bolk=1.38054e-23; {Boltzmannova konstanta}

var lam5:double;

begin
 lam5:=lam*lam*lam*lam*lam;
 b:=8.0*pi*h*c/lam5/(exp(h*c/lam/bolk/tep)-1.0);
end;

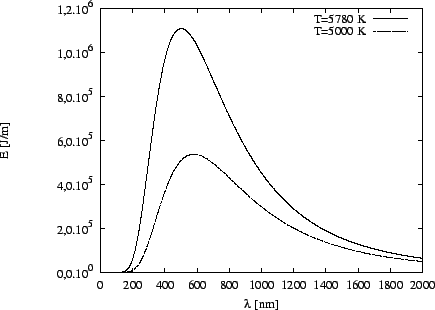
Na obrázku je graf závislosti Planckovy funkce na vlnové délce pro teploty $5\, 000 \,\mathrm{K}$ a $5\,780\,\mathrm{K}$. Jsou patrné dva závěry. V celém intervalu vlnových délek platí, že spektrální hustota vyzařovaná tělesem s vyšší teplotou je větší. Patrný je posuv maxima obou křivek, pro vyšší teploty směrem k nižším vlnovým délkám.

Řešení úlohy 14.6
Na stránce http://cdsweb.u-strasbg.fr zvolíme "VizieR", jako "Wavelength" zvolíme "X-ray", jako "Astronomical keywords" zvolíme "Stars:early-type" a zadáme hledání ("Find Catalogues"). Vybereme katalog odpovídající úloze, "ROSAT all-sky survey catalogue of OB stars", "Detections". V prohledávání zvoleného katalogu zaškrtneme třídění ("Sort") podle pozorované hustoty toku rentgenového záření ("Apparent X-ray flux"). Aby se třídění opravdu provedlo, je nutné ještě zadat vhodnou podmínku ("Constraint", vzhledem k velikosti pozorovaného toku např. "$<0$"). Je nutné navíc zvolit "Output Order" jako "-". Z tabulky zjistíme, že nejjasnějšími hvězdami spektrálních typů O nebo B v rentgenovém oboru jsou X Per ( $F_\mathrm{x}=1,0.10^{-13}\,\mathrm{W}.\mathrm{m}^{-2}$), $\beta$ Per ( $F_\mathrm{x}=6,6.10^{-14}\,\mathrm{W}.\mathrm{m}^{-2}$), $\gamma$ Cas ( $F_\mathrm{x}=3,0.10^{-14}\,\mathrm{W}.\mathrm{m}^{-2}$), $\theta^1$ Ori ( $F_\mathrm{x}=2,8.10^{-14}\,\mathrm{W}.\mathrm{m}^{-2}$) a $\iota$ Ori ( $F_\mathrm{x}=2,5.10^{-14}\,\mathrm{W}.\mathrm{m}^{-2}$).

Řešení úlohy 14.7
Na uvedené stránce získáme potřebná data. Zdroj pro identifikaci čar nalezneme v katalozích CDS, http://cdsweb.u-strasbg.fr/cats/Cats.htx, zvolíme hledání "identification spectrum", katalog "VI/26 Identification list of lines in Stellar Spectra (Moore, 1959)" a jeho novou verzi "VI/71A Revised version of the ILLSS Catalogue (Coluzzi 1993-1999)", v prohledávání zvoleného katalogu ("VizieR query form") zadáme podmínku pro vlnové délky jako " $>5870\;\&\&\;<5930$" a identifikujeme čáry. Výsledný graf je na následujícím obrázku.

Řešení úlohy 14.8
Na obrázku je graf jednotlivých závislostí.

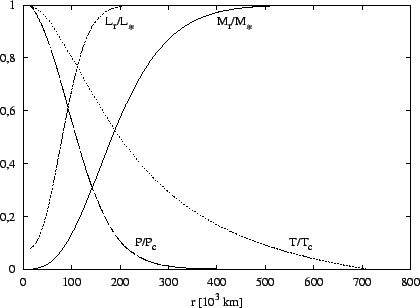
Řešení úlohy 14.9
Centrální tlak a teplota hvězdy se sluneční hmotností ( $T_c=1,4.10^{7}\,\mathrm{K}$, $\rho_c=7,7.10^{4}\,\mathrm{kg}.\mathrm{m}^{-3}$) jsou vyšší než odpovídající hodnoty pro hvězdu s hmotností nižší ( $T_c=1,1.10^{7}\,\mathrm{K}$, $\rho_c=6,8.10^{4}\,\mathrm{kg}.\mathrm{m}^{-3}$).

Řešení úlohy 14.10
Hvězda s vyšším obsahem kovů má nižší efektivní teplotu ( $T_{\rm ef}=5\,280\,\mathrm{K}$) a zářivý výkon ( $L=0,76104 L_{\odot}$) než hvězda s chemickým složením shodným se Sluncem (viz. příklad 14.8). Důvodem je větší opacita látky hvězdy s vyšším obsahem kovů. U hvězdy s menším zářivým výkonem je nižší centrální teplota.

Řešení úlohy 14.11
Charakteristiky hvězd hlavní posloupnosti získané programem STATSTAR jsou uvedeny v tabulce. Přesné hodnoty parametrů hvězd jsou uvedeny pouze pro získání daného modelu stavby hvězdy (jsou vybrány tak, aby byly splněny příslušné okrajové podmínky diferenciálních rovnic popisujících stavbu hvězd) a nemají tedy astrofyzikální smysl.

$M$ [$M_{\odot}$]	$L$ [$L_{\odot}$]	$T_{\mathrm{ef}}$[K]
$0,50$	$0,0213005$	$2321,4$
$0,70$	$0,129867$	$3523,0$
$1,00$	$0,86071$	$5500,2$
$1,50$	$6,39$	$8726,4$
$2,00$	$22,5809$	$11218,4$
$3,00$	$116,58$	$15007,3$
$4,00$	$341,1$	$17904,0$
$7,00$	$2260,2$	$24074,0$
$10,00$	$6641,5$	$28263,6$
$13,00$	$13789,5$	$31493,0$

Řešení úlohy 14.12
Na uvedené stránce zvolíme např. "Catalogues ", hledání podle "Allende Prieto Lambert", zvolíme hledaný článek a získáme potřebný soubor (např. zvolíme stahování prostřednictvím http, soubor "table1.dat.gz". Formát souboru je popsán v popisu katalogu. Pomocí získaného souboru nakreslíme HR diagram (následující obrázek).

Řešení úlohy 14.13
Na uvedené stránce zvolíme např. "Catalogues ", hledání podle "Schaller" a zvolíme hledaný článek. Například prostřednictvím http získáme potřebné soubory "table*" a nakreslíme graf. Odhadovaná hmotnost hvězdy $\sigma$ Ori E je $9\,M_{\odot}$.

Řešení úlohy 14.14
Pro Sahovo rozdělení platí

$$\frac{N_{1}}{N_0}=\frac{2 B_{1}}{n_e B_0} \left(\frac{2\pi m_\mathrm{e} k T}{h^2}\right)^{3/2}{\mathrm e}^{-\chi_i/kT},$$

kde $N_{1}$ je koncentrace iontu, $N_0$ neutrálního atomu, $B_1$ a $B_0$ jsou příslušné rozdělovací funkce a $\chi_i$ ionizační potenciál. Celková koncentrace atomů vodíku $N=N_{1}+N_0$. Pro získání hodnot v grafu je možné použít následující program sahav:

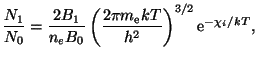
program sahav;

var tep,nel,x:double;
    i:integer;

function saha(tep,nel:double):double;

const em=9.10956e-31;   {hmotnost elektronu}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      h=6.6256e-34;     {Planckova konstanta}
      exc=13.598;       {excitacni energie H v eV}
      enab=1.6022e-19;  {naboj elektronu}

var b1,b2,x:double;

begin
 b1:=2.0;
 b2:=1.0;
 x:=2.0*pi*em*bolk*tep/h/h;
 saha:=2.0*b2*sqrt(x)*x*exp(-exc*enab/bolk/tep)/nel/b1;
end;

begin
 tep:=1000;
 nel:=1.0e17;
 for i:=1 to 200 do
 begin
  tep:=tep+100.0;
  x:=saha(tep,nel);
  writeln(tep,1.0/(1.0+x));
 end;
end.

Na obrázku je výsledný graf.

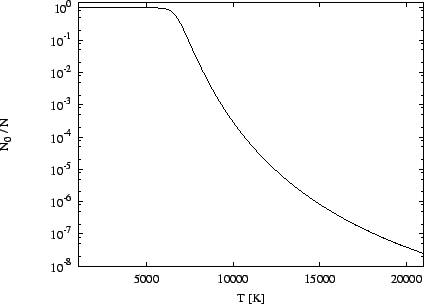
Řešení úlohy 14.15
Využijeme výsledku předcházejícího příkladu (10.6) pro výpočet relativního zastoupení neutrálního vodíku. Pro výpočet podílu koncentrace vodíku na druhé hladině k celkovému množství neutrálního vodíku využijeme Boltzmannovy rovnice

$$\frac{N_{B}}{N_A}=\frac{g_B}{g_A}{\mathrm e}^{-\chi_{AB}/kT},$$

kde $N_{B}$ a je koncentrace atomu vodíku na druhé hladině a $N_A$ celková koncentrace neutrálního vodíku, $g_B$ a $g_A$ jejich statistické váhy, $\chi_{AB}$ excitační energie.

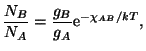
Pro získání grafu na obrázku je možné použít následující program sahav2,

program sahav2;

const em=9.10956e-31;   {hmotnost elektronu}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      h=6.6256e-34;     {Planckova konstanta}
      exc=13.598;       {excitacni energie H v~eV}
      enab=1.6022e-19;  {naboj elektronu}

var tep,nel,x,n,gh,g2,x2:double;
    i:integer;

function saha(tep,nel:double):double;

const em=9.10956e-31;   {hmotnost elektronu}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      h=6.6256e-34;     {Planckova konstanta}
      exc=13.598;       {excitacni energie H v~eV}
      enab=1.6022e-19;  {naboj elektronu}

var g1,g2,x:double;

begin
 g1:=2.0;
 g2:=1.0;
 x:=2.0*pi*em*bolk*tep/h/h;
 saha:=2.0*g2*sqrt(x)*x*exp(-exc*enab/bolk/tep)/nel/g1;
end;

begin
 tep:=1000;
 nel:=1.0e20;
 gh:=2.0;
 n:=2.0;
 g2:=2.0*n*n;
 for i:=1 to 200 do
 begin
  tep:=tep+100.0;
  x:=saha(tep,nel);
  x2:=g2/gh*exp(-exc*enab/bolk/tep*(1.0-1.0/n/n));
  writeln(tep,x2/(1.0+x));
 end;
end.

ve kterém jsme využili funkci saha z předcházejícího příkladu.

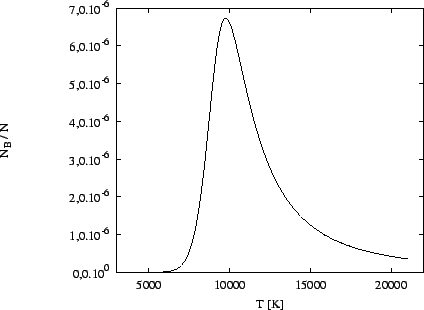
Tvar křivky je dán jednak tím, že s rostoucí teplotou roste podíl excitovaných atomů vodíku k atomům v základním stavu. Proto křivka pro nízké teploty zprvu roste. Pro vyšší teploty se začíná vodík ionizovat, ubývá celkového množství atomů vodíku v základním stavu a tedy i podíl atomů vodíku na druhé hladině klesá.

Balmerovy čáry vznikají přechody mezi hladinou s kvantovým číslem $2$ a vyššími hladinami. Proto jsou za dané elektronové koncentrace nejvýraznější právě pro teplotu $T\cong 9800{\rm K}$.

Řešení úlohy 14.16
Pro výpočet závislosti vystupující intenzity na tloušťce vrstvy je možné použít program izotv:

program izotv;

var i: integer;
    b,tau,int,i0: double;

begin
 b:=2.0;
 i0:=3.0;
 for i:=1 to 100 do
 begin
  tau:=(i-1)/10.0;
  int:=i0*exp(-tau)+b*(1.0-exp(-tau));
  writeln(tau,int);
 end;
end.

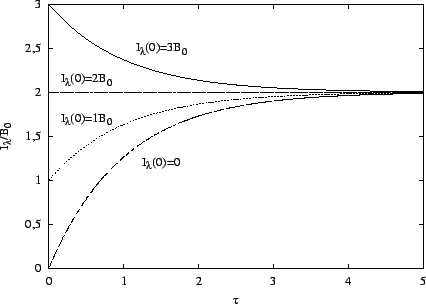
Nejprve diskutujme případ, kdy na vrstvu nedopadá žádné záření ( $I_{\lambda}(0)=0$, viz. obrázek) Je patrné, že pro opticky tenké vrstvy je intenzita záření závislá na optické hloubce lineárně, pro rostoucí optické hloubky vrstvy se blíží k Planckově funkci. Obecně, pro libovolnou intenzitu dopadajícího záření platí, že intenzita vystupujícího záření pro případ opticky tenké vrstvy je přibližně rovna intenzitě dopadajícího záření. Příkladem opticky tenkých prostředí mohou být například některé hvězdné větry. Naopak, pro opticky tlustá prostředí intenzita vystupujícího záření se blíží Planckově funkci, nezávisí tedy na intenzitě dopadajícího záření a na optické hloubce vrstvy. Příkladem opticky tlustého prostředí může být sluneční atmosféra v čáře $\mathrm{H}_{\alpha}$.

Řešení úlohy 14.17
Pro intenzitu záření černého tělesa je možné odvodit vztah

$$B(\lambda,T)=\frac{2 h c^2}{\lambda^5}\frac{1}{{\mathrm e}^{hc/\lambda k T}-1}.$$

Se znalostí předcházejícího příkladu 10.8 je možné napsat následující program prof, který vypočítá záření emitované vrstvou:

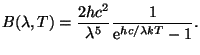
program prof;

const a=1.0;
      tau0=1.0;
      ts=5780.0;
      tl=5000.0;
      lam0=5000.0e-10;

var i,j:integer;
    i0,u:double;
      
function voigt(v,agam:double):double; {Voigtova funkce} 
 begin
  if(abs(v)>8.0) then
    voigt:=agam/sqrt(pi)/(agam*agam+v*v)/sqrt(pi)
   else
    voigt:=(exp(-v*v)+agam/sqrt(pi)/(agam*agam+v*v))/sqrt(pi);
 end;

function b(tep,lam:double):double;

const h=6.6256e-34;     {Planckova konstanta}
      c=2.99792e8;      {rychlost svetla}
      bolk=1.38054e-23; {Boltzmannova konstanta}

var lam5:double;

begin
 lam5:=lam*lam*lam*lam*lam;
 b:=2.0*h*c*c/lam5/(exp(h*c/lam/bolk/tep)-1.0);
end;

function profil(a,tau0,u:double):double;
var tau: double;
begin
 tau:=tau0*voigt(u,a);
 profil:=b(ts,lam0)*exp(-tau)+b(tl,lam0)*(1.0-exp(-tau));
end;

begin
 u:=-10.0;
 i0:=profil(a,tau0,u);
 for i:=0 to 2000 do
  begin
   u:=u+0.01;
   writeln(u,profil(a,tau0,u)/i0);
  end;
end.

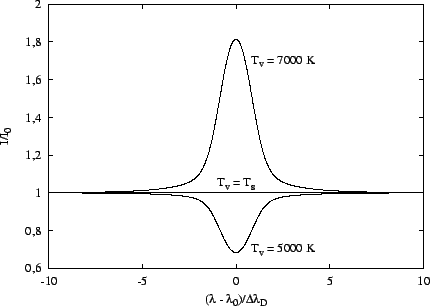
Na předchozím obrázku jsou nakresleny profily čar, získané uvedeným programem. Jednotlivým případům uvedeným v zadání se budeme věnovat podrobněji. Obecně však platí (viz. výsledek předcházejícího příkladu 10.8), že v centru čáry, kde je optická hloubka vrstvy vysoká, se pozorovaná intenzita blíží Planckově funkci s teplotou rovnou teplotě vrstvy. Naopak v křídlech čáry, kde je optická hloubka vrstvy nízká, se pozorovaná intenzita blíží Planckově funkci s teplotou rovnou teplotě dopadajícího záření. Tento poznatek je také klíčem k pochopení jednotlivých případů. V případě a), kdy je teplota vrstvy nižší než teplota dopadajícího záření, je také hodnota Planckovy funkce v centru čáry nižší, než hodnota Planckovy funkce dopadajícího záření a my pozorujeme absorpční čáry. Tento model je možné použít pro vysvětlení vzniku absorpčních čar např. ve viditelném spektru Slunce. Opačný jev nastává v případě b), kdy je teplota vrstvy vyšší než teplota dopadajícího záření. Tento model popisuje vznik emisních čar. V případě c), kdy je teplota vrstvy rovna teplotě dopadajícího záření se vrstva spolu s okolním zářením nachází ve stavu termodynamické rovnováhy a žádné čáry nepozorujeme.

Řešení úlohy 14.18
Pro výpočet ekvivalentní šířky čáry v závislosti na její optické hloubce, je možné využít program krivrust:

program krivrust;

const taumin=0.5;
      taumax=100.0;
      ntau=300;
      nlam=200;
      u0=-800.0;
      a=1.0;
      ts=5780.0;
      tl=5000.0;
      lam0=5000.0e-10;

var x,gam: double;
    i,j:integer;
    tau0,w,it,i0,u,dltau,dlam:double;

begin
 tau0:=taumin;
 dltau:=exp((ln(taumax)-ln(taumin))/(ntau-1));
 dlam:=2.0*abs(u0)/nlam;
 for j:=0 to ntau do
  begin
   u:=u0;
   i0:=profil(a,tau0,u);
   w:=0;
   for i:=0 to nlam do
    begin
     it:=(i0-profil(a,tau0,u))/i0;
     u:=u+dlam;
     if(i>0) and (i<nlam) then
       w:=w+it
     else
       w:=w+0.5*it;
   end;
   w:=w*dlam;
   writeln(tau0,' ',w);
   tau0:=tau0*dltau;
 end;
end.

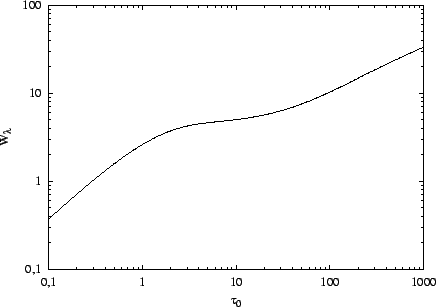
Funkce voigt, b a profil zde nevypisujeme, všechny je možné převzít z předcházející úlohy 10.9 . Na obrázku je graf, který byl získán uvedeným programem.

Řešení úlohy 14.19
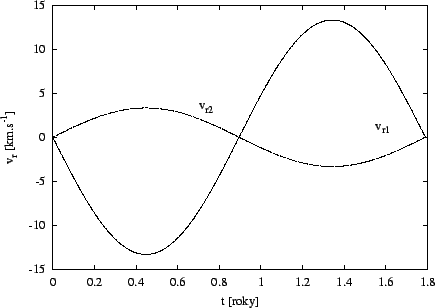
Vzájemná rychlost obou hvězd je dána vztahem $v^2=G(M_1+M_2)/a$, pro radiální rychlost první hvězdy platí $v_{r1}=-\sin i \sin\theta \mu v/M_1$, kde $\theta$ je úhel mezi přímkou spojující hvězdy a směrem k pozorovateli. Pro vykreslení křivky radiálních rychlostí na obrázku lze použít program radrych:

program radrych;

const au=1.496e11;
      ms=1.989e30;
      a=2.0*au;
      m1=0.5*ms;
      m2=2.0*ms;
      i=pi/6.0;
      ntheta=1000;
      g=6.67e-11;
      rok=60.0*60.0*24.0*365.0;

var si,theta,v,v1,v2,mu,p,t:double;
    j:integer;

begin
 si:=sin(i);
 mu:=m1*m2/(m1+m2);
 p:=2.0*pi*sqrt(a*a*a/g/(m1+m2));
 for j:=0 to ntheta do
 begin
  theta:=2.0*pi*j/ntheta;
  v:=sqrt(g*(m1+m2)/a);
  v1:=-v*mu/m1*sin(theta)*si;
  v2:=v*mu/m2*sin(theta)*si;
  t:=j/ntheta*p/rok;
  writeln(t,' ',v1,' ',v2);
 end;
end.

Řešení úlohy 14.20
Potenciál $\Phi=-\frac{GM_1}{r_1}-\frac{GM_2}{r_2}-\frac{s^2\omega^2}{2}$, kde $s$ je vzdálenost od osy rotace, vyjádříme v bezrozměrných veličinách, $\frac{\Phi}{G(M_1+M_2)/a}=-\frac{M_1}{M_1+M_2}\frac{a}{r_1}-\frac{M_2}{M_1+M_2}\frac{a}{r_2}-\frac{1}{2} \frac{s^2}{a^2}$. Pro vykreslení můžeme například v programu Gnuplot použít následující skript:

m1=0.85
m2=0.17
x1=m2/(m1+m2)
x2=m1/(m1+m2)
mcos(a,b)=a/b
r1(x,y)=(x1*x1+x*x+y*y+2*x1*(x*x+y*y)**0.5*mcos(x,(x*x+y*y)**0.5))**0.5
r2(x,y)=(x2*x2+x*x+y*y-2*x2*(x*x+y*y)**0.5*mcos(x,(x*x+y*y)**0.5))**0.5
splot -(m1/r1(x,y)+m2/r2(x,y)+0.5*(m1+m2)*(x*x+y*y))/(m1+m2)

Výsledek je na předchozím obrázku. Lagrangeovy body $L_1$, $L_2$ a $L_3$ jsou sedlovými body potenciálu, v Lagrangeových bodech $L_4$ a $L_5$ dosahuje potenciál svého maxima.

Řešení úlohy 14.21
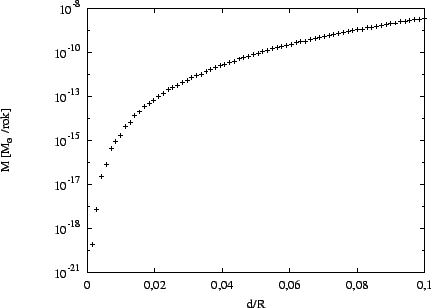
Pro výpočet závislosti rychlosti přenosu hmoty $\dot M$ na tloušťce vrstvy hvězdy, která přesahuje Rocheovu plochu, je možné použít program phmot, který načítá model atmosféry (bez hlavičky) vypočtený programem STATSTAR:

program phmot;

const rhv=7.11e8;       {polomer hvezdy}
      rcgs=0.01;        {prepocet CGS}
      rhocgs=1000.0;    {prepocet CGS}
      ms=1.989e30;      {hmotnost Slunce}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      mh=1.6735e-27;    {hmotnost atomu vodiku}


var dm,r,qm,lr,t,p,rho: double;
    i: integer;

begin
 for i:=1 to 424 do
 begin
  readln(r,qm,lr,t,p,rho);
  dm:=pi*rhv*(rhv-r*rcgs)*rho*rhocgs*sqrt(3.0*bolk*t/mh);
  writeln(1.0-r*rcgs/rhv,dm/ms);
 end;
end.

Řešení úlohy 14.22
Na adrese http://adsabs.harvard.edu zvolíme "Search", "Astronomy and Astrophysics Search" a jako "Object name" zadáme "CQ UMa". Zvolíme hledání, "Send Query". Podle názvu zvolíme článek, který se týká hledání periody, získáme jeho pdf verzi a vyhledáme určenou periodu. Například v článku Improvement of the Period of CQ UMa autorů Jozefa Žižňovského a Zdeňka Mikuláška (IBVS, číslo 4259, strana 1) nalezneme periodu $2,4499141\pm0,0000038\,\mathrm{dne}$.

Řešení úlohy 14.23
Na adrese http://cds.u-strasbg.fr zvolíme "Catalogs", zadáme hledání "GG Lup" a zvolíme článek Clausen a kol. 1993, Astron. Astrophys. Suppl. Ser. 101, 563 (například volba FTP). Získáme soubor table1, pomocí něhož nakreslíme světelnou křivku.

Řešení úlohy 14.24
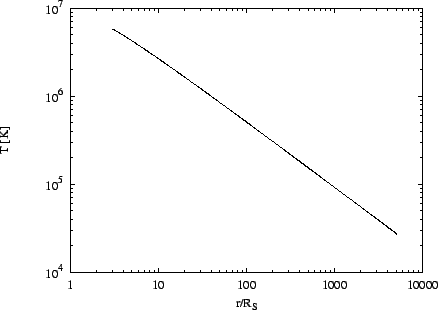
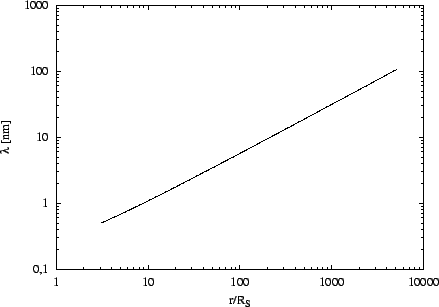
Pro získání grafů je možné použít program disk:

program disk;

const ms=1.989e30;      {hmotnost Slunce}
      m=3.82*ms;

      g=6.67e-11;       {gravitacni konstanta}
      dmdt=1.0d14;
      sig=5.67051d-8;   {konstanta Stefan-Boltzmannova zakona}
      c=2.99792e8;      {rychlost svetla}
      b=0.0029;         {konstanta Wienova zakona}

var rs,tdisk,r,dr,ddr,t,mlam: double;
    i: integer;

begin
 rs:=2.0*g*m/c/c;
 tdisk:=3.0*g*m*dmdt/8.0/pi/sig/rs/rs/rs;
 tdisk:=sqrt(sqrt(tdisk));
 r:=3.0*rs;
 for i:=1 to 500 do
 begin
  r:=1.015*r;
  dr:=sqrt(rs/r);
  ddr:=sqrt(dr);
  t:=tdisk*ddr*ddr*ddr*sqrt(sqrt(1.0-dr));
  mlam:=b/t;
  writeln(r/rs,t,mlam*1.0e9);
 end;
end.

Řešení úlohy 14.25
Na stránce CDS http://cdsweb.u-strasbg.fr/cats/Cats.htx, na které je možné hledat astronomické katalogy, zadáme hledání "TYCHO". Zvolíme "I/197A Tycho Input Catalogue, Revised version (Egret+ 1992)", ("VizieR query form"). Pro úsporný výpis zvolíme "Maximum Entries per table" jako "unlimited", "Output layout" jako "tiny ascii" a zaškrtneme výpis pouze položky "Vmag". Jako kritérium pro hledání zadáváme např. "4+/-0.5" (postupujeme např. po celých magnitudách). Na základě počtu nalezených hvězd získáme následující obrázek.

Počet hvězd $N$ v kouli o poloměru $r$ je úměrný $N\sim r^3$. Vzdálenost, do které uvidíme hvězdy hvězdné velikosti $m$, které mají stejnou absolutní hvězdnou velikost $M$ je dána vztahem $m - M = 5\log r - 5$, kde $r$ je vyjádřeno v parsecích. Počet hvězd je tedy úměrný $N\sim10^{0,6(m-M+5)}$, počet hvězd s danou hvězdnou velikostí je úměrný $\mathrm{d}N/\mathrm{d}m\sim10^{0,6m}$. Tato křivka je nakreslena nepřerušovanou čarou na obrázku. Slabých hvězd pozorujeme nápadně méně, než by to odpovídalo uvažovanému modelu, důvodem je vliv mezihvězdné extinkce.

Řešení úlohy 14.26
Abychom získali zářivý výkon v radiovém oboru, musíme integrovat zářivý tok přes všechny frekvence a sečíst tok na kouli o poloměru $250\,\mathrm{Mpc}$. S použitím lichoběžníkového pravidla je možné napsat program agn:

program agn;

const nf=10;
      d=250.0;
      mpc=3.09e22;

var nu,nus,f,fs,lr,r: double;
    i: integer;

function des(x: double) : double;
begin
 des:=exp(x*ln(10.0));
end;

begin
 lr:=0.0;
 for i:=1 to nf do
 begin
  read(nu,f);
  nu:=des(nu);
  f:=des(f);
  if(i > 0) then lr:=lr+0.5*(fs+f)*(nu-nus);
  fs:=f;
  nus:=nu;
 end;
 r:=d*mpc;
 lr:=4.0*pi*r*r*lr;
 writeln(lr);
end.

Zářivý výkon galaxie Cygnus A v rádiovém oboru je $9\,10^{37}\,\mathrm{J}.\mathrm{s}^{-1}$, což je o šest řádů více, než je zářivý výkon galaxie M31 v rádiové oblasti a asi desetkrát více než zářivý výkon naší Galaxie ve všech oborech elektromagnetického spektra.

Řešení úlohy 14.27
Na adrese http://adsabs.harvard.edu zvolíme "Search", "Astronomy and Astrophysics Search" a jako autory (na každý řádek jednoho) napíšeme Penzias a Wilson, zaškrtněte AND, klepneme na "Send Query". Hledaným článkem je A Measurement of Excess Antenna Temperature at 4080 Mc/s (Astrophysical Journal, číslo 142, strana 419). Kliknutím na odkaz vybraného článku pak získáte jeho abstrakt, je možné získat přímo samotný článek.

Řešení úlohy 14.28
Článek získáme například na adrese http://adsabs.harvard.edu. Z tabulky 4 tohoto článku převezmeme vzdálenosti galaxií $D_Z$, z tabulky 5 jejich radiální rychlosti ( $V_\mathrm{Shapley}$). Získanými daty proložíme přímku a spočteme hodnotu Hubbleovy konstanty $H=77\pm4\,\mathrm{km}.\mathrm{s}^{-1}.\mathrm{Mpc}^{-1}$.