Řešení úlohy 5.1
Řešení úlohy 5.3
Balmerova série, čtvrtá čára
![]() s
s
![]() , fialová barva.
, fialová barva.
Řešení úlohy 5.4
Dosadíme do vztahu
![]() , čáry leží v submilimetrovém pásmu v infračervené oblasti spektra a nemůžeme je z povrchu Země pozorovat.
, čáry leží v submilimetrovém pásmu v infračervené oblasti spektra a nemůžeme je z povrchu Země pozorovat.
Řešení úlohy 5.5
![]() , podmínku splňuje čára
Balmerovy série
, podmínku splňuje čára
Balmerovy série
![]() o vlnové délce
o vlnové délce
![]() , pro kterou
platí
, pro kterou
platí
![]() .
.
Řešení úlohy 5.6
![]() ,
,
![]() ,
přechod A
,
přechod A
![]() B,
B,
![]() ,
,
![]() , přechod A
, přechod A
![]() C,
C,
![]() ,
,
![]() .
.
Řešení úlohy 5.8
![]() ,
,
![]() ,
,
![]() ,
,
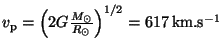 .
Hodnoty rychlostí atomů vodíku a železa jsou nižší než hodnota únikové rychlosti
Slunce, proto zůstávají v koróně.
.
Hodnoty rychlostí atomů vodíku a železa jsou nižší než hodnota únikové rychlosti
Slunce, proto zůstávají v koróně.
Řešení úlohy 5.9
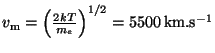 ,
,
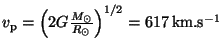 , coulombovská přitažlivá síla elektronů k protonům způsobuje, že zůstávají v koróně Slunce.
, coulombovská přitažlivá síla elektronů k protonům způsobuje, že zůstávají v koróně Slunce.
Řešení úlohy 5.10
![]() ,
,
![]() . Hledaná vzdálenost je
. Hledaná vzdálenost je
![]() ,
,
![]() ,
,
![]() , úhly
určíme
, úhly
určíme
![]() ,
,
![]() .
Dosazením dostaneme
.
Dosazením dostaneme
![]() .
.
Řešení úlohy 5.11
Počet vrypů určíme dosazením do vztahu
![]() .
.
Řešení úlohy 5.12
Velikost gravitačního rudého posuvu
![]() porovnáme s velikostí
dopplerovského posuvu
porovnáme s velikostí
dopplerovského posuvu
![]() .
.
Řešení úlohy 5.13
Pro příčný Dopplerův jev, při zanedbání členů s vyššími mocninami,
platí vztah
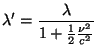 , předpokládáme platnost
vztahu
, předpokládáme platnost
vztahu
![]() .
.
a)
![]() ,
,
![]() ,
,
b)
![]() ,
,
![]() .
.
V prvním případě příčný Dopplerův jev nemusíme uvažovat, v druhém ano.
Řešení úlohy 5.14
Z atomové fyziky je znám vztah
![]() ,
,
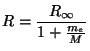 . Při zanedbání malých veličin
dostaneme
. Při zanedbání malých veličin
dostaneme
![]() . Dosadíme
. Dosadíme
![]() a obdržíme
a obdržíme
![]() , tedy
, tedy
![]() , izotopem je deuterium.
, izotopem je deuterium.
Řešení úlohy 5.16
![]() ,
jednotlivé hodnoty šířek
,
jednotlivé hodnoty šířek
![]() se liší členem
se liší členem ![]() .
Pro čáru K CaII a jednotlivé teploty dostaneme
.
Pro čáru K CaII a jednotlivé teploty dostaneme
![]() ,
,
![]() .
Při fyzikální podmínkách ve fotosférách je teplotní rozšíření zpravidla dominantní. S rostoucí hmotností atomů klesá šířka čar.
.
Při fyzikální podmínkách ve fotosférách je teplotní rozšíření zpravidla dominantní. S rostoucí hmotností atomů klesá šířka čar.
Řešení úlohy 5.18
Pro vodíkovou čáru
![]() je
je
![]() , což je hodnota velmi malá, srovnatelná s přirozeným rozšířením spektrální čáry. Při narůstání hustoty atomů ve fotosféře se srážkové rozšíření zvyšuje.
, což je hodnota velmi malá, srovnatelná s přirozeným rozšířením spektrální čáry. Při narůstání hustoty atomů ve fotosféře se srážkové rozšíření zvyšuje.
Řešení úlohy 5.19
Vedle jiných příčin je rozhodující rozšíření čar vyvolané
tepelným pohybem atomů. Při teplotě
![]() je rychlost vodíkových
atomů asi
je rychlost vodíkových
atomů asi
![]() . Vlnová délka
. Vlnová délka
![]() viditelného světla se při takové
rychlosti posouvá o
viditelného světla se při takové
rychlosti posouvá o
![]() . Šířka
čáry je tak
. Šířka
čáry je tak
![]() . Ve skutečnosti jsou však
balmerovské čáry mnohem širší než činí tento hrubý odhad, důležité je
rozšíření křídel čar srážkami. Jednotlivé části zejména mohutných spektrálních
čar vznikají v různých vrstvách atmosféry.
. Ve skutečnosti jsou však
balmerovské čáry mnohem širší než činí tento hrubý odhad, důležité je
rozšíření křídel čar srážkami. Jednotlivé části zejména mohutných spektrálních
čar vznikají v různých vrstvách atmosféry.
Řešení úlohy 5.20
Dosazením obdržíme
![]() .
.
Řešení úlohy 5.23
Rotační obvodová
rovníková rychlost je rovna
![]() . Rozšíření čáry
podmíněné rotací je dáno vztahem
. Rozšíření čáry
podmíněné rotací je dáno vztahem
![]() , po dosazení
obdržíme
, po dosazení
obdržíme
![]() .
.
Řešení úlohy 5.25
Okrajové ztemnění zmenšuje rozšíření čar spojené s rotací hvězdy.
Řešení úlohy 5.26
Využijeme vztah pro Zeemanův jev
![]() , odkud
, odkud
![]() .
.
Řešení úlohy 5.27
Pro spektroskopickou zjistitelnost musí platit
![]() ,
tedy
,
tedy
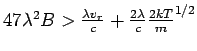 , dosazením obdržíme
, dosazením obdržíme
![]() .
.
Řešení úlohy 5.28
Pro rozšíření vyvolané Zeemanovým jevem vyjádřeným v SI platí:
![]() , odtud
, odtud
![]() . Jev
bude spektroskopicky zjistitelný, při
. Jev
bude spektroskopicky zjistitelný, při
![]() ,
tedy
,
tedy
![]() , po dosazení obdržíme:
, po dosazení obdržíme:
![]() .
.
Řešení úlohy 5.29
Ze vztahu
![]() stanovíme
stanovíme
![]() . Různost vlnových délek rozštěpených čar odpovídá rychlosti
. Různost vlnových délek rozštěpených čar odpovídá rychlosti
![]() .
.
Řešení úlohy 5.30
![]() ,
,
![]()
![]() . Nelze tedy spektroskopicky rozšíření čar zjistit.
. Nelze tedy spektroskopicky rozšíření čar zjistit.