Řešení úlohy 6.1
pp řetězec:
Řešení úlohy 6.1
pp řetězec:
![]() ,
,
![]() , tedy
, tedy
![]() . Pro
3
. Pro
3![]() proces:
proces:
![]() ,
,
![]() , tudíž
, tudíž
![]() .
.
Řešení úlohy 6.2
Obdobným postupem jako u první úlohy určíme
![]() .
.
Řešení úlohy 6.3
Užijeme vztahy
![]()
![]() a dosadíme do stavové rovnice pro
ideální plyn
a dosadíme do stavové rovnice pro
ideální plyn
![]() . Odtud obdržíme
. Odtud obdržíme
![]() .
.
Řešení úlohy 6.4
Počet atomů
![]() je
je
![]() , kde
, kde
![]() ,
,
![]() je počet atomů chlóru,
je počet atomů chlóru,
![]() je tok
neutrin na Zemi. Odtud obdržíme
je tok
neutrin na Zemi. Odtud obdržíme
![]() .
Při experimentu je nezbytné použít
.
Při experimentu je nezbytné použít
![]() o hmotnosti
o hmotnosti
![]() ,
,
![]() . V této úloze je
. V této úloze je ![]() molekulární hmotnost.
molekulární hmotnost.
Řešení úlohy 6.5
Z uvedených hodnot centrálních teplot vyplývá, že jde o hvězdy
s velkými hmotnostmi, kde probíhá CNO cyklus, u něhož množství uvolňované energie
![]() . Hledaný poměr je
. Hledaný poměr je
![]() , k jehož výpočtu
využijeme vztah
, k jehož výpočtu
využijeme vztah
![]() , tedy
, tedy
![]() .
.
Řešení úlohy 6.6
Vyjdeme z vlastností fotonového plynu. Počet fotonů v objemové
jednotce je
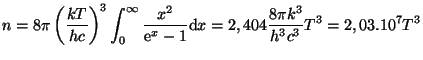 ,
hustotu energie fotonů vyjádříme
,
hustotu energie fotonů vyjádříme
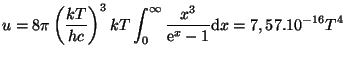 . Pro střední energii
připadající na jeden foton lze odvodit
. Pro střední energii
připadající na jeden foton lze odvodit
![]() . Pro
tlak záření platí
. Pro
tlak záření platí
![]() , intenzitu záření
vyjádříme
, intenzitu záření
vyjádříme
![]() . Propočítané výsledky shrneme v tabulce:
. Propočítané výsledky shrneme v tabulce:
| Vlastnosti | Povrch Slunce
|
Střed Slunce
|
| Střední energie fotonu
|
||
| Hustota fotonů
|
|
|
| Hustota energie
|
|
|
| Tlak záření
|
|
|
| Intenzita záření
|
|
|
Řešení úlohy 6.7
Počet fotonů vyzářených Sluncem za l sekundu je dán vztahem
![]() . Počet
neutrin se střední energií lze odhadnout takto. V první úloze jsme vypočetli
energii
. Počet
neutrin se střední energií lze odhadnout takto. V první úloze jsme vypočetli
energii
![]() uvolňovanou při syntéze
vodík
uvolňovanou při syntéze
vodík
![]() helium. Slunce za jednu sekundu vyzáří
helium. Slunce za jednu sekundu vyzáří
![]() . Tedy za jednu sekundu vznikne přibližně
. Tedy za jednu sekundu vznikne přibližně ![]() heliových jader. Při vzniku jednoho heliového jádra vzniknou dvě neutrina, proto
za každou sekundu vznikne
heliových jader. Při vzniku jednoho heliového jádra vzniknou dvě neutrina, proto
za každou sekundu vznikne ![]() elektronových neutrin. Poměr počtu fotonů
a neutrin je přibližně
elektronových neutrin. Poměr počtu fotonů
a neutrin je přibližně ![]() .
.
Řešení úlohy 6.8
V zjednodušeném přiblížení platí pro tlakovou sílu na jednotkovou
plochu tedy tlak
![]() , po dosazením číselných
hodnot hmotnosti a poloměru Slunce a průměrné hustoty
, po dosazením číselných
hodnot hmotnosti a poloměru Slunce a průměrné hustoty
![]() dostaneme pro tlak
dostaneme pro tlak
![]() . Podle
standardních modelů Bahcalla je ve skutečnosti centrální tlak o řád vyšší.
. Podle
standardních modelů Bahcalla je ve skutečnosti centrální tlak o řád vyšší.
Řešení úlohy 6.9
Při
![]() lze zjednodušeně předpokládat
lze zjednodušeně předpokládat
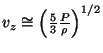 , kde
, kde
![]() . Po dosazení obdržíme
. Po dosazení obdržíme
![]() .
Poloměrem Slunce projdou zvukové vlny za
.
Poloměrem Slunce projdou zvukové vlny za
![]() .
.
Řešení úlohy 6.11
![]() ,
,
![]() . Podstatný je tlak plynu, tlak záření je zanedbatelný.
. Podstatný je tlak plynu, tlak záření je zanedbatelný.
Řešení úlohy 6.12
Dosazením do podmínky degenerace
![]() zjistíme, že není splňována. V současné fázi vývoje Slunce je v jeho nitru degenerace nepodstatná.
zjistíme, že není splňována. V současné fázi vývoje Slunce je v jeho nitru degenerace nepodstatná.
Řešení úlohy 6.13
Úvahy lze zjednodušit následujícím způsobem. Pro gravitační sílu platí
![]() . Tlaková síla je dána součinem tlaku
. Tlaková síla je dána součinem tlaku
![]() a povrchu
a povrchu ![]() , tudíž
, tudíž
![]() . Obě síly za normálních podmínek klesají s rozměry
hvězdy, při jejich rovnosti nastane rovnovážný stav. Obě síly klesají stejně při koeficientu
. Obě síly za normálních podmínek klesají s rozměry
hvězdy, při jejich rovnosti nastane rovnovážný stav. Obě síly klesají stejně při koeficientu
![]() .
.
Diskutujme dvě možnosti, nejprve nechť
![]() . V tomto případě je
tlaková křivka strmější než gravitační. Jestliže hvězda náhodně zvětší své rozměry, převládne gravitační síla a hvězda se smrští. Zmenší-li hvězda své rozměry,
převládne tlaková síla a hvězda zvětší svůj rozměr. Shrnuto změny objemu hvězdy nemají za následek její rozpad.
. V tomto případě je
tlaková křivka strmější než gravitační. Jestliže hvězda náhodně zvětší své rozměry, převládne gravitační síla a hvězda se smrští. Zmenší-li hvězda své rozměry,
převládne tlaková síla a hvězda zvětší svůj rozměr. Shrnuto změny objemu hvězdy nemají za následek její rozpad.
V případě
![]() je situace odlišná. Jestliže hvězda náhodně
zvětší své rozměry, převládne tlaková síla a dojde ke zvětšování objemu. Hvězda
se stane nestabilní, například může odhodit vnější vrstvy. Zmenší-li své rozměry dojde ke gravitačnímu kolapsu.
je situace odlišná. Jestliže hvězda náhodně
zvětší své rozměry, převládne tlaková síla a dojde ke zvětšování objemu. Hvězda
se stane nestabilní, například může odhodit vnější vrstvy. Zmenší-li své rozměry dojde ke gravitačnímu kolapsu.
Hvězdná látka bílých trpaslíků se vyznačuje polytropním indexem blízkým
![]() , ten se však mění s hmotností bílého trpaslíka. Při kritické Chandrasekharově hmotnosti přibližně
, ten se však mění s hmotností bílého trpaslíka. Při kritické Chandrasekharově hmotnosti přibližně
![]() má hodnotu právě
má hodnotu právě
![]() a bílý trpaslík se stává nestabilní.
a bílý trpaslík se stává nestabilní.
Řešení úlohy 6.14
Po dosazení
![]() ,
,
![]() .
.
Řešení úlohy 6.15
a) Dosadíme do rovnice kontinuity
![]() .
.
b)
![]()
c)
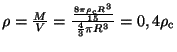 .
.
Řešení úlohy 6.16
a) Při konstatní hustotě platí
![]() ,
,
![]() . Dosadíme
. Dosadíme ![]() do rovnice hydrostatické rovnováhy
do rovnice hydrostatické rovnováhy
![]() a integrujeme od středu
a integrujeme od středu
![]() k povrchu
k povrchu ![]() . Obdržíme
. Obdržíme
![]() ;
;
![]() .
.
b) Užijeme výrazy ![]() ,
, ![]() a
a ![]() z předchozích úloh, budeme
integrovat rovnici hydrostatické rovnováhy
z předchozích úloh, budeme
integrovat rovnici hydrostatické rovnováhy
![]() ;
;
![]() .
.
Řešení úlohy 6.17
Pro hmotnost
![]() obdržíme
obdržíme
![]() . Efektivní
teplotu B0 V lze odhadnout na přibližně
. Efektivní
teplotu B0 V lze odhadnout na přibližně
![]() . Poloměr hvězdy je
. Poloměr hvězdy je
![]() , tudíž střední hustota
, tudíž střední hustota
![]() .
.
Řešení úlohy 6.18
Pro gravitační zrychlení platí
![]() , pro
, pro
![]() ,
,
![]() , poměr zrychlení je
roven
, poměr zrychlení je
roven
![]() . Střední hustoty určíme
ze vztahu
. Střední hustoty určíme
ze vztahu
![]() , poměr hustot je roven
, poměr hustot je roven
![]() .
.
Řešení úlohy 6.20
![]() ,
,
![]() ,
,
![]() ,
,
![]() Protože platí
Protože platí ![]() dostaneme
dostaneme
![]() .
.
Řešení úlohy 6.21
Postupným dosazováním podle jednotlivých případů do vztahu
z předcházející úlohy obdržíme ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Řešení úlohy 6.23
Gradient tlaku je dán vztahem
![]() , kde
, kde ![]() je střední hodnota
opacity. Rovnice hydrostatické rovnováhy
je střední hodnota
opacity. Rovnice hydrostatické rovnováhy
![]() je
uvažovaná na povrchu hvězdy, tedy pro
je
uvažovaná na povrchu hvězdy, tedy pro ![]() . Dosadíme a upravíme:
. Dosadíme a upravíme:
![]() , což je hodnota maximálního zářivého výkonu,
při kterém je hvězda ještě ve stavu zářivé rovnováhy. Užívají se rovněž i tyto
vztahy:
, což je hodnota maximálního zářivého výkonu,
při kterém je hvězda ještě ve stavu zářivé rovnováhy. Užívají se rovněž i tyto
vztahy:
![]() .
.
Řešení úlohy 6.24
Dosadíme do vztahu pro Eddingtonův limitní zářivý výkon
![]() . U hvězd nízké hmotnosti na hlavní posloupnosti, viz řešení úlohy č. 10, lze tlak záření zanedbávat.
. U hvězd nízké hmotnosti na hlavní posloupnosti, viz řešení úlohy č. 10, lze tlak záření zanedbávat.
Řešení úlohy 6.25
Podmínku
![]() můžeme přepsat
můžeme přepsat
![]() . Odtud při využití vztahu hmotnost - zářivý výkon obdržíme
. Odtud při využití vztahu hmotnost - zářivý výkon obdržíme
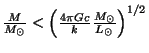 .
Dosazením
.
Dosazením
![]() .
.
Řešení úlohy 6.26
Rovnice hydrostatické rovnováhy má v zadaném
případě tvar
![]() .
Pro zjednušení budeme předpokládat konstantnost dodatečného povrchového
gravitačního zrychlení na povrchu Slunce v průběhu smršťování
.
Pro zjednušení budeme předpokládat konstantnost dodatečného povrchového
gravitačního zrychlení na povrchu Slunce v průběhu smršťování
![]() , očekávaná změna poloměru je přibližně
, očekávaná změna poloměru je přibližně
![]() . Ze vztahu
. Ze vztahu
![]() stanovíme čas
stanovíme čas
![]() , tedy asi 17 minut. Změna poloměru by byla pozorovatelná ze Země.
, tedy asi 17 minut. Změna poloměru by byla pozorovatelná ze Země.
Řešení úlohy 6.27
Předpokládáme ze zadání platnost zářivé rovnováhy ve hvězdě. Tok
zářivé energie jednotkovou plochou sféry o poloměru ![]() je dán vztahem
je dán vztahem
![]() . Energie absorbovaná ve zvoleném objemovém elementu je
. Energie absorbovaná ve zvoleném objemovém elementu je
![]() . Tlakový gradient je
. Tlakový gradient je
![]() , kde
, kde
![]() . Dosazením obdržíme rovnici pro teplotní gradient.
. Dosazením obdržíme rovnici pro teplotní gradient.
Řešení úlohy 6.28
Konvekce je dominatní při splnění podmínky
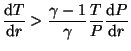 , což lze zapsat
, což lze zapsat
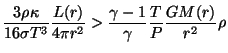 . Po dosazení
obdržíme
. Po dosazení
obdržíme
![]() , tedy podmínka nastolení konvekce je splňována.
, tedy podmínka nastolení konvekce je splňována.
Řešení úlohy 6.29
Minimální kritická hodnota zářivého výkonu na jednotku hmotnosti přenášená konvekcí je dána vztahem
![]() , kde
, kde
![]() . Po číselném dosazení obdržíme
. Po číselném dosazení obdržíme
![]() . Protože propočítaná hodnota je větší, přenos konvekcí nenastává.
. Protože propočítaná hodnota je větší, přenos konvekcí nenastává.
Řešení úlohy 6.30
Střední volná dráha fotonu je
![]() . Při
centrální teplotě Slunce
. Při
centrální teplotě Slunce
![]() a přibližné
povrchové teplotě
a přibližné
povrchové teplotě
![]() je střední teplotní
gradient roven
je střední teplotní
gradient roven
![]() . Pro šíření fotonu nitrem Slunce k povrchu platí
. Pro šíření fotonu nitrem Slunce k povrchu platí
![]() , kde
, kde ![]() udává počet absorpcí a emisí. Dosazením dostaneme
udává počet absorpcí a emisí. Dosazením dostaneme
![]() . Každá emise respektive reemise proběhne průměrně za
. Každá emise respektive reemise proběhne průměrně za
![]() , tedy za
, tedy za
![]() roků dospěje foton k povrchu.
roků dospěje foton k povrchu.
Řešení úlohy 6.31
Adiabatická rychlost zvuku je dána vztahem
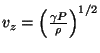 , tlak vyjádříme z rovnice hydrostatické rovnováhy za předpokladu
konstantní hustoty
, tlak vyjádříme z rovnice hydrostatické rovnováhy za předpokladu
konstantní hustoty
![]() , pro tlak obdržíme
, pro tlak obdržíme
![]() . Pulsační perioda je dána vztahem
. Pulsační perioda je dána vztahem
![]()
![$ 2\int_0^R{\left[\frac{2}{3}\gamma\pi G\rho\left(R^2-r^2\right)\right]^{-1/2}}{{\mathrm d}r} \Rightarrow
\Pi\sim\left(\frac{3\pi}{2\gamma G\rho}\right)^{1/2}$](img675.gif) .
.