Řešení úlohy 8.1
Podle III. Keplerova zákona platí
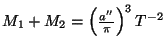 .
Určíme
.
Určíme
Řešení úlohy 8.1
Podle III. Keplerova zákona platí
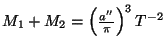 .
Určíme
.
Určíme ![]() a stanovíme vzdálenost
a stanovíme vzdálenost
![]() .
.
Řešení úlohy 8.2
![]() rad
rad![]() . Ano, neboť úhlová vzdálenost mezi hvězdami převyšuje tuto hodnotu.
. Ano, neboť úhlová vzdálenost mezi hvězdami převyšuje tuto hodnotu.
Řešení úlohy 8.3
Dosazením do III. Keplerova zákona stanovíme součet hmotností obou
složek
![]() ,
kde
,
kde
![]() . Pomocí vztahu
. Pomocí vztahu
![]() nalezneme
nalezneme
![]() a
a
![]() . Zářivé výkony nalezneme ze vztahu
. Zářivé výkony nalezneme ze vztahu
![]() ,
,
![]() ,
,
![]() .
.
Řešení úlohy 8.4
Pro
měřitelnost rozštěpení spektrálních čar
![]() podmíněného
dopplerovským posuvem je třeba, aby rychlost hvězd převyšovala střední
kvadratickou rychlost pohybu atomů vodíku ve fotosférách hvězd. Dostaneme již
známou podmínku
podmíněného
dopplerovským posuvem je třeba, aby rychlost hvězd převyšovala střední
kvadratickou rychlost pohybu atomů vodíku ve fotosférách hvězd. Dostaneme již
známou podmínku
![]() , kde
v případě pohybu dvojhvězd platí
, kde
v případě pohybu dvojhvězd platí
![]() . Rychlost vypočteme ze vztahu
. Rychlost vypočteme ze vztahu
![]() . Po dosazení obdržíme podmínku
. Po dosazení obdržíme podmínku
![]() .
.
Řešení úlohy 8.5
Lineární velikost velké poloosy je
![]() AU, součet hmotností je
roven
AU, součet hmotností je
roven
![]() , tedy
, tedy
![]() . Observačně zjištěné hodnoty
hmotností jednotlivých složek jsou
. Observačně zjištěné hodnoty
hmotností jednotlivých složek jsou
![]() a
a
![]() . První hvězda je červeným trpaslíkem z nejspodnější části hlavní posloupnosti zatímco druhá hvězdy je již hnědým trpaslíkem.
. První hvězda je červeným trpaslíkem z nejspodnější části hlavní posloupnosti zatímco druhá hvězdy je již hnědým trpaslíkem.
Řešení úlohy 8.6
Pro poměr hmotností obou složek platí
![]() .
Z dopplerovského posuvu určíme radiální rychlosti
.
Z dopplerovského posuvu určíme radiální rychlosti
![]() ,
,
![]() . Poloměry drah jsou
. Poloměry drah jsou
![]() ,
,
![]() .
Velká poloosa
.
Velká poloosa
![]() . Pro
celkovou hmotnost soustavy platí
. Pro
celkovou hmotnost soustavy platí
![]() .
Jednotlivé hmotnosti složek jsou
.
Jednotlivé hmotnosti složek jsou
![]() a
a
![]() .
.
Řešení úlohy 8.7
Obdobně jako u předcházejících úloh určíme rychlosti obou složek
![]() ,
,
![]() . Dále určíme velikosti jednotlivých
poloos
. Dále určíme velikosti jednotlivých
poloos
![]() ,
,
![]() . Velká poloosa
. Velká poloosa
![]() . Při výpočtu celkové hmotnosti soustavy dosadíme do
III. Keplerova zákona
. Při výpočtu celkové hmotnosti soustavy dosadíme do
III. Keplerova zákona
![]() , hmotnost jednotlivých
složek určíme ze vztahu
, hmotnost jednotlivých
složek určíme ze vztahu
![]() ,
,
![]()
Řešení úlohy 8.8
Velikosti velkých poloos jsou
![]() a
a
![]() . Velká
poloosa
. Velká
poloosa
![]() . Celkovou hmotnost soustavy určíme
z III. Keplerova zákona
. Celkovou hmotnost soustavy určíme
z III. Keplerova zákona
![]() . Dále dosadíme do
vztahů pro zákrytové proměnné
. Dále dosadíme do
vztahů pro zákrytové proměnné
![]() a
a
![]() , kde
, kde ![]() a
a ![]() jsou
poloměry složek. Poloměr první složky
jsou
poloměry složek. Poloměr první složky
![]() a druhé
složky
a druhé
složky
![]() . Hmotnosti jednotlivých složek určíme ze
vztahu
. Hmotnosti jednotlivých složek určíme ze
vztahu
![]() ,
,
![]() .
.
Řešení úlohy 8.9
Součet hmotností obou složek vyjádřený v jednotkách hmotnosti
Slunce určíme za vztahu
![]() , obdržíme
, obdržíme
![]() . Jednotlivé hmotnosti stanovíme pomocí
vztahu
. Jednotlivé hmotnosti stanovíme pomocí
vztahu
![]() ,
,
![]() a
a
![]() .
.
Řešení úlohy 8.10
Budeme zjednodušeně předpokládat, že kolem hvězdy obíhá pouze jedna
planeta s hmotností Jupitera. Střední oběžná rychlost pohybu extrasolární
planety ![]() by tudíž byla
by tudíž byla
![]() . Protože
. Protože
![]() že očekávaná rychlost pohybu hvězdy
bude
že očekávaná rychlost pohybu hvězdy
bude
![]() v dráhové rovině exoplanety. Požadovaná
přesnost optických metod určování radiálních rychlostí by měla být ještě
v dráhové rovině exoplanety. Požadovaná
přesnost optických metod určování radiálních rychlostí by měla být ještě
![]() větší, v roce 1998 již byla dostatečná, dosahovala zhruba
větší, v roce 1998 již byla dostatečná, dosahovala zhruba
![]() .
.
Řešení úlohy 8.11
Oběžnou dobu stanovíme z III. Keplerova zákona
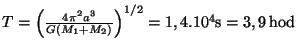 . Rychlost
první složky je
. Rychlost
první složky je
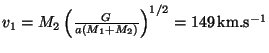 ,
druhé
,
druhé
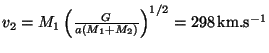 . Hodnota
. Hodnota
![]() Při
přenosu hmoty od složky s menší hmotností ke složce s větší hmotností narůstá
oběžná doba
Při
přenosu hmoty od složky s menší hmotností ke složce s větší hmotností narůstá
oběžná doba ![]() a zvětšuje se velká poloosa
a zvětšuje se velká poloosa ![]() dvojhvězdy.
dvojhvězdy.
Řešení úlohy 8.12
Vyjdeme ze vztahu pro velikost momentu hybnosti
![]() , odkud vyjádříme
, odkud vyjádříme
![]() . Rovnici logaritmujeme a
derivujeme (logaritmická derivace) a
odvodíme
. Rovnici logaritmujeme a
derivujeme (logaritmická derivace) a
odvodíme
![]() .
.
Řešení úlohy 8.13
Vyjdeme z III. Keplerova zákona, ze kterého logaritmickou derivací
dostaneme
![]() . Dosazením
. Dosazením
![]() obdržíme
obdržíme
![]() .
.
Řešení úlohy 8.14
Předpokládáme platnost zákona zachování hmotnosti a dráhového momentu
hybnosti při přenosu hmoty, tedy
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
Z posledně uvedeného dostaneme
.
Z posledně uvedeného dostaneme
![]() , odkud při platnosti vztahu
, odkud při platnosti vztahu
![]() obdržíme
obdržíme
![]() .
.
Řešení úlohy 8.15
Při nárůstu oběžné doby je hmota přenášena od druhé složky ![]() k první
k první ![]() . Ze vztahu
. Ze vztahu
![]() určíme
určíme
![]() .
.
Řešení úlohy 8.16
Dosadíme do vztahu
![]() .
.
Řešení úlohy 8.17
Celková mechanická energie fyzikálního
dvojhvězdného systému o hmotnostech jednotlivých složek ![]() ,
, ![]() je
je ![]() ,
vzdálenost složek je
,
vzdálenost složek je ![]() . Jde o gravitačně vázanou soustavu, platí
. Jde o gravitačně vázanou soustavu, platí
![]() . Pro rychlosti platí:
. Pro rychlosti platí:
![]() . Předpokládejme,
že u první hvězdy proběhla sférickosymetrická exploze, při níž nedošlo ke
změně rychlosti
. Předpokládejme,
že u první hvězdy proběhla sférickosymetrická exploze, při níž nedošlo ke
změně rychlosti ![]() a nechť pozůstatek první složky po výbuchu má hmotnost
a nechť pozůstatek první složky po výbuchu má hmotnost
![]() . Platí
. Platí
![]() . Celková mechanická energie systému po
explozi je
. Celková mechanická energie systému po
explozi je
![]() .
Pro gravitačně vázanou soustavu platí
.
Pro gravitačně vázanou soustavu platí ![]() . Dále platí
. Dále platí
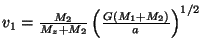 a
a
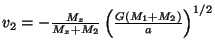 . Dosazením
obdržíme pro
. Dosazením
obdržíme pro
![]() . Podmínka
pro zachování dvojhvězdného systému je
. Podmínka
pro zachování dvojhvězdného systému je
![]() .
.
Řešení úlohy 8.18
Dosadíme do závěrečné nerovnice předchozí úlohy,
![]() ,
,
![]() ,
,
![]() . Tudíž je splněna podmínka
. Tudíž je splněna podmínka
![]() .
.
Řešení úlohy 8.19
Dosadíme
![]() ,
,
![]() ,
,
![]() , podmínka
, podmínka
![]() není splněna, dvojhvězdný systém se rozpadne.
není splněna, dvojhvězdný systém se rozpadne.
Řešení úlohy 8.20
Pro pohyb v dráhové rovině má integrál energie tvar
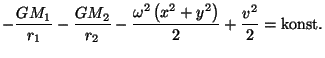
Řešení úlohy 8.22
Zářivý výkon, především v rtg. oblasti záření, je
přibližně roven rychlosti ztráty gravitační potenciální energie plynu při
akreci,
![]() a
a
![]() .
Dosazením získáme zářivý výkon
.
Dosazením získáme zářivý výkon
![]() . Pro zářivý
výkon pulsaru platí
. Pro zářivý
výkon pulsaru platí
![]() , odtud
určíme
, odtud
určíme
![]() .
.
Řešení úlohy 8.23
Z III. Keplerova zákona
![]() určíme velikost velké poloosy
určíme velikost velké poloosy
![]() . Oběžná dráha pulsaru je kruhová,
. Oběžná dráha pulsaru je kruhová,
![]() . Dopplerovský posuv
způsobený radiálním pohybem je
. Dopplerovský posuv
způsobený radiálním pohybem je
![]() ,
,
![]() . Úplná
amplituda změny periody je
. Úplná
amplituda změny periody je
![]() .
.
Řešení úlohy 8.24
Z III. Keplerova zákona stanovíme velikost velké poloosy
![]() . Vzdálenost pulsaru od hmotného
středu je
. Vzdálenost pulsaru od hmotného
středu je
![]() . Rychlost oběžného pohybu
pulsaru je
. Rychlost oběžného pohybu
pulsaru je
![]() .
V důsledku Dopplerova jevu se mění perioda pulsací, její relativní
změna je
.
V důsledku Dopplerova jevu se mění perioda pulsací, její relativní
změna je
![]() . Jev pozorujeme jako zpožďování příchodu pulsů. Na dráze
. Jev pozorujeme jako zpožďování příchodu pulsů. Na dráze
![]() je maximální hodnota zpožďování
je maximální hodnota zpožďování
![]() .
.
Řešení úlohy 8.25
Dosazením do uvedených vztahů dostaneme pro gravitační zářivý výkon soustavy
![]() , což je numericky hodnota nesrovnatelně menší než gravitační vazebná energie soustavy
, což je numericky hodnota nesrovnatelně menší než gravitační vazebná energie soustavy
![]() . Pro změnu oběžné doby obdržíme
. Pro změnu oběžné doby obdržíme
![]() , tedy hodnotu odpovídající téměř přesně naměřené.
, tedy hodnotu odpovídající téměř přesně naměřené.