Závěrečná stadia vývoje hvězd - řešení

Řešení úlohy 11.1
V přiblížení klasické fyziky platí vztahy: , $E=h\nu\Rightarrow m=\frac{h\nu}{c^2}$ . Gravitační potenciální energie na povrchu hvězdy je $E_p=-G\frac{Mh\nu}{Rc^2}$ . Celková energie je $E_c=h\nu\left(1-\frac{GM}{c^2R}\right)$ . Energie detekovaného fotonu na Zemi je $h\nu'=h\nu\left(1-\frac{GM}{c^2R}\right)$ , $\Delta\nu=\nu-\nu'$ . Úpravou pro hmotnost hvězdy obdržíme $M=\frac{\Delta\nu}{\nu}\frac{c^2R}{G}$ , nebo při využití vlnových délek $M=\frac{\Delta\lambda }{\lambda}\frac{c^2R}{G}$ , kde jsme volili $\left\vert\frac{\Delta\nu}{\nu}\right\vert=\left\vert\frac{\Delta\lambda}{\lambda}\right\vert$ . V rámci OTR lze změnu vlnové délky záření vyjádřit přibližně $\frac{\Delta\lambda }{\lambda}=\left(1-\frac{2GM}{c^2R}\right)^{-1/2}-1\cong\frac{GM}{c^2R}$ .

Řešení úlohy 11.2
Dosadíme do uvedeného vztahu: a) ${T_2}/{T_1}=1,000212$ , b) ${T_2}/{T_1}=1,191828$ , c) ${T_2}/{T_1}\rightarrow\infty$ .

Řešení úlohy 11.3
Vyjádříme gravitační potenciální enegii $E_p=-\frac{3}{5}\frac{GM^2}{R}=-2,3.10^{43}\mathrm{J}$ , kinetickou energii $E_k=\frac{3}{2}NkT=2,1.10^{41}\mathrm{J}$ , tedy $\vert\langle E_k\rangle\vert < \vert\langle E_p \rangle\vert$ . Hydrostatická rovnováha u bílých trpaslíků je udržována tlakem degenerovaného elektronového plynu, nikoliv tlakem plynu vyvolaným tepelným pohybem. Předpokládanou dobu existence stanovíme $T=\frac{E_k}{L}=5,4.10^{16}\mathrm{s}\cong10^9\,$ roků.

Řešení úlohy 11.4
Vyjdeme z rovnice hydrostatické rovnováhy: $\frac{{\mathrm d}P}{{\mathrm d}r}=-\frac{M}{r^2}\rho$ , $\frac{{\mathrm d}}{{\mathrm d}r}\rightarrow\frac{1}{R}$ . Platí $\frac{P}{R}\sim\frac{M}{R^2}\rho$ , $\rho^{\frac{2}{3}}\sim\frac{M}{R}\Rightarrow R\sim M^{-\frac{1}{3}}$ . S rostoucí hmotností bílého trpaslíka se zmenšuje poloměr a hustota především v centrální části do poloměru se zvětšuje.

Řešení úlohy 11.5
Z uvedených údajů lze odhadovat střední hmotnost bílých trpaslíků za předpokladu platnosti vztahu pro gravitační rudý posuv na $z=\frac{\Delta\lambda }{\lambda}=\frac{GM}{c^2 R}$ , $M = 1,3.10^{30}\,\mathrm{kg}=0,65\,M_{\odot}$ .

Řešení úlohy 11.6
Pro teplotu nitra platí $\displaystyle T_i=\left[\frac{LZ\left(1+X\right)}{7,3.10^4\mu} \frac{M_{\odot}}{M}\right]^{2/7}=2,8.10^7\,\mathrm{K}$

Řešení úlohy 11.7
V limitním případě, jestliže neutrino neodnáší energii, užijeme relativistické vyjádření kinetické energie pro elektron $m_{\mathrm{e}}c^2\left[\left(1-\frac{v^2}{c^2}\right)^{-1}-1\right]=\left(m_{\mathrm{n}}-m_{\mathrm{p}}-m_{\mathrm{e}}\right)c^2$ . Pro nerelativistické elektrony je rychlost $\displaystyle v\cong\frac{h}{2\pi m_{\mathrm{e}}}n_{\mathrm{e}}^{1/3}\cong\fra... ...thrm{e}}}\left[\left(\frac{Z}{A}\right)\frac{\rho}{m_{\mathrm{H}}}\right]^{1/3}$ , odtud $\displaystyle \left(\frac{m_{\mathrm{e}}}{m_{\mathrm{n}}-m_{\mathrm{p}}}\right... ...e}}^2c^2}\left[\left(\frac{Z}{A}\right)\frac{\rho}{m_{\mathrm{H}}}\right]^{2/3}$ . Pro hustotu obdržíme $\displaystyle \rho\cong\frac{Am_{\mathrm{H}}}{Z}\left(\frac{2\pi m_{\mathrm{e}... ...eft(\frac{m_{\mathrm{e}}}{m_{\mathrm{n}}-m_{\mathrm{p}}}\right)^2 \right]^{3/2}$
$\cong2,3.10^{10}\mathrm{kg}.\mathrm{m}^{-3}$ při předpokladu $\frac{A}{Z}=1$ pro vodík.

Řešení úlohy 11.8
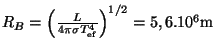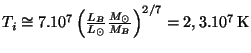$R_B=\left(\frac{L}{4\pi\sigma T_{\mathrm{ef}}^4}\right)^{1/2}=5,6.10^6\mathrm{m}$ tudíž $0,008\,R_{\odot}$ . Úpravou vztahu pro gravitační rudý posuv dostaneme $M_B = \frac{c^2}{G}R_B\frac{\Delta\lambda }{\lambda} = 2,1 . 10^{ 30}\mathrm{kg}$ , tedy $1,03\,M_{\odot}$ . Průměrná hustota $\rho=2,86.10^9\,\mathrm{kg}.\mathrm{m}^{-3}$ . Teplotu nitra stanovíme ze vztahu $T_i\cong7.10^7\left(\frac{L_B}{L_{\odot}}\frac{M_{\odot}}{M_B}\right)^{2/7}=2,3.10^7\,\mathrm{K}$ . 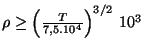Podmínka degenerace stanovuje $K_1\rho^{\frac{5}{3}}\geq \frac{\mbox{\rsfsm R}\rho T}{\mu}$ , odkud po částečném dosazení obdržíme $\rho \geq\left(\frac{T}{7,5.10^4}\right)^{3/2}\,10^3$ . Nerovnice dává pro $\rho \geq 5,4.10^6\,\mathrm{kg}.\mathrm{m}^{-3}$ , tudíž podmínka degenerace elektronů je splněna.

Řešení úlohy 11.9
Poloměr určíme 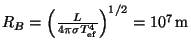$R_B=\left(\frac{L}{4\pi\sigma T_{\mathrm{ef}}^4}\right)^{1/2}=10^7\,\mathrm{m}$ tedy $0,015\,R_{\odot}$ . Hmotnost $M_B = \frac{c^2}{G}R_B\frac{\Delta\lambda }{\lambda} = 8 . 10^{ 29}\,\mathrm{kg}$ , přibližně $0,43\,M_{\odot}$ .

Řešení úlohy 11.10
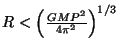Pro hmotný bod na rovníku rotující neutronové hvězdy musí platit . Dosazením obdržíme $R<\left(\frac{GMP^2}{4\pi^2}\right)^{1/3}$ , $R<20\,\mathrm{km}$ .

Řešení úlohy 11.11
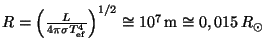Zářivý výkon stanovíme ze vztahu $L=10^{0,4\left(4,75-M_{\mathrm{bol}}\right)}\cong0,017\,L_{\odot}$ . Poloměr určíme ze vztahu $R=\left(\frac{L}{4\pi\sigma T_{\mathrm{ef}}^4}\right)^{1/2}\cong10^7\,\mathrm{m}\cong0,015\,R_{\odot}$ .

Řešení úlohy 11.12
Z Wienova posunovacího zákona určíme $\lambda_\mathrm{max}=\frac{b}{T}=1,44\,\mathrm{nm}$ , zářivý výkon stanovíme ze Stefanova-Boltzmannova zákona $L=4\pi R^2\sigma T_{\mathrm{ef}}^4=1,14.10^{27}\,\mathrm{W}$ .

Řešení úlohy 11.13
Dosadíme charakteristiky typických neutronových hvězd $M=2,8.10^{30}\,\mathrm{kg}=1,4\,M_{\odot}$ , $R =1,5.10^4\,\mathrm{m}=15\,\mathrm{km}$ .

Řešení úlohy 11.14
Pulsar je zdrojem elektromagnetického záření v širokém intervalu frekvencí. Na Zemi je nejprve přijímáno záření o vyšších kmitočtech, následně teprve záření o nižších kmitočtech. Velikost tohoto časového posunu, tzv. disperzní míra, závisí na koncentraci volných elektronů v mezihvězdném prostředí ve směru pulsaru a na vzdálenosti pulsaru. Při řešení využijeme již upravený vzorec, ve kterém je časový rozdíl vyjádřen v sekundách, hustota elektronů $n_{\mathrm{e }}$ je dána jejich počtem v $\mathrm{m}^3$ vzdálenost je v $\pc$ a frekvence a jsou v MHz. Platí vztah $\Delta t=4,15.10^{-3}\,n_{\mathrm{e }}d\left(\frac{1}{f_1^2}-\frac{1}{f_2^2}\right)$ , odkud pro vzdálenost dostaneme $d = 2 000\,\pc$ . Tzv. disperzní míra $DM=\int_0^dn_{\mathrm{e }}{\mathrm d}l=5,6.10^7\,\pc.\mathrm{m}^{-3}$ .

Řešení úlohy 11.15
Ze vztahu $\Delta t=4,15.10^{-3}\,n_{\mathrm{e }}d\left(\frac{1}{f_1^2}-\frac{1}{f_2^2}\right)$ určíme $n_{\mathrm{e }} = 2,5.10^4\,\mathrm{m}^{-3}$ .

Řešení úlohy 11.16
$\frac{{\mathrm d}E_{\mathrm{rot}}}{{\mathrm d}t}=-\frac{8}{5}\pi^2MR^2P^{-3}\frac{{\mathrm d}P}{{\mathrm d}t} = 5.10^{31}\,\mathrm{W}$ což odpovídá zářivému výkonu Krabí mlhoviny. Lze také vyjádřit změnu rotační kinetické energie za sekundu, tedy $\Delta E_{\mathrm{rot}} =\frac{4\pi^2MR^2}{5P^2}-\frac{4\pi^2MR^2}{5\left(P+\D... ...)-\left(\frac{1}{P^2}-\frac{2\Delta P}{P^3}\right)\right] = 10^{32}\,\mathrm{J}$ . Samotná Krabí mlhovina má zářivý výkon asi $5 . 10^{ 31}\,\mathrm{ W}$ .

Řešení úlohy 11.17
Rotační kinetická energie je dána vztahem $E_{\mathrm{rot}}=\frac{1}{2}I\omega^2$ , $I=\frac{2}{5}MR^2$ . Předpokládejme, že veškerá energie se přeměňuje na záření, platí zákon zachování energie: $\frac{{\mathrm d}E_{\mathrm{zar}}}{{\mathrm d}t}+\frac{{\mathrm d}E_{\mathrm{rot}}}{{\mathrm d}t}=0$ . Dále platí $L=\frac{{\mathrm d}E_{\mathrm{zar}}}{{\mathrm d}t}=-\frac{{\mathrm d}E_{\mathrm{rot}}}{{\mathrm d}t}=\frac{8}{5}\pi^2MR^2P^{-3}\frac{{\mathrm d}P}{{\mathrm d}t}$ . Odtud dostaneme $\frac{{\mathrm d}P}{{\mathrm d}t}=\frac{5}{8\pi^2}\frac{LP^3}{MR^2}$ , po dosazení obdržíme pro nárůst periody rotace $\frac{{\mathrm d}P}{{\mathrm d}t}=4.10^{-13}$ . Přibližný odhad stáří pulsaru dává $t\cong\frac{0,033}{4 . 10^{ - 13}}\cong 10^{11}\cong 3 .10^3\,$ roků. Ve skutečnosti je stáří pulsaru asi $10^{3}\,$ roků.

Řešení úlohy 11.18
Zářivý výkon rotujícího magnetického dipólu je 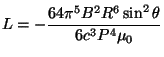$L =\displaystyle -\frac{64\pi^5B^2R^6\sin^2\theta}{6c^3P^4\mu_0}$ . Předpokládáme, že $\frac{{\mathrm d}E_{\mathrm{rot}}}{{\mathrm d}t}=-\frac{8}{5}\pi^2MR^2P^{-3}\frac{{\mathrm d}P}{{\mathrm d}t}$ . Za předpokladu, že rotační kinetická energie se plně přeměňuje na záření platí $-\frac{8}{5}\pi^2MR^2P^{-3}\frac{{\mathrm d}P}{{\mathrm d}t}=-4\pi^2IP^{-3}\frac{{\mathrm d}P}{{\mathrm d}t}=\frac{64\pi^5B^2R^6\sin^2\theta}{6c^3P^4\mu_0}$ . 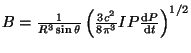Pro hodnotu magnetické indukce dostáváme $B = \frac{1}{R^3\sin\theta} \left(\frac{3c^2}{8\pi^3}IP\frac{{\mathrm d}P}{{\mathrm d}t}\right)^{1/2}$ . Dosazením obdržíme hodnotu $B\cong 8 . 10^8\,\mathrm{T}$ , což je řádově srovnatelné s hodnotou zjištěnou z pozorování $B = 4 . 10^8\,\mathrm{T}$ .

Řešení úlohy 11.19
$\epsilon=h\frac{c}{\lambda}=2\,\mathrm{eV}$ , $E_e^2=\frac{\epsilon}{B}\Rightarrow E_e=10^{12}\,\mathrm{eV}$ .

Řešení úlohy 11.20
Postup obdobný jako v předcházejících úlohách, ${\mathrm d}P/{\mathrm d}t = 1,2 . 10^{ - 13}$ , $t \cong 5 . 10^4\,$ roků.

Řešení úlohy 11.21
Pro náš výpočet zvolme zářivý výkon $10^{ 30}\,\mathrm{W}$ . Poloměr vypočteme ze vztahu $R=\left(\frac{L}{4\pi\sigma T^4}\right)^{1/2}$ . Numerická velikost akrečního disku kolem černé díry $2 R \cong 20\,\mathrm{km}$ . Nechť na objekt o poloměru a hmotnosti dopadá hmota tempem ${\mathrm d}M/{\mathrm d}t$ za s. Produkovaná gravitační potenciální energie je $\frac{{\mathrm d}E_{\mathrm{grav}}}{{\mathrm d}t}=G\frac{M}{R}\frac{{\mathrm d}M}{{\mathrm d}t}$ . Jestliže energie se přeměňuje na záření se 100% účinností, dostaneme ze vztahu $L=G\frac{M}{R}\frac{{\mathrm d}M}{{\mathrm d}t}$ , $\frac{{\mathrm d}M}{{\mathrm d}t}=\frac{RL}{GM}= 7,5 . 10^{ 13}\,\mathrm{kg}.\mathrm{s}^{-1}$ . Reálnější předpoklad účinnosti je asi 50%.

Řešení úlohy 11.22
Po dosazení hodnot obdržíme $\frac{{\mathrm d}E_{\mathrm{rot}}}{{\mathrm d}t}\cong -5.10^{31}\,\mathrm{W}$ .

Řešení úlohy 11.23
Akreční zářivý výkon je dán vztahem $L\cong G\frac{M}{R}\frac{{\mathrm d}M}{{\mathrm d}t}$ , odtud určíme $\frac{{\mathrm d}M}{{\mathrm d}t}=\frac{RL}{GM}= 6.10^{14}\,\mathrm{kg}.\mathrm{s}^{-1}\cong10^{-8}\,M_{\odot}.\mathrm{rok}^{ - 1}$ .

Řešení úlohy 11.24
Ze vztahu $L=-\frac{8}{5}\pi^2MR^2P^{-3}\frac{{\mathrm d}P}{{\mathrm d}t}$ určíme . Odtud $\frac{1}{P}\frac{{\mathrm d}P}{{\mathrm d}t}=1.10^{-9}\,\mathrm{s}^{-1}$ . Pulsar by se rychle zastavil.

Řešení úlohy 11.25
Pro černou díru je velikost úhlového momentu hybnosti $L_{\max}=\frac{GM^2}{c}=$
$1,7.10^{42}\,\mathrm{kg}.\mathrm{m}.\mathrm{s}^{-2}$ , pro pulsar $L=m\omega r^2=1,1.10^{42}\,\mathrm{kg}.\mathrm{m}.\mathrm{s}^{-2}$ . Úhlové momenty hybnosti jsou u obou těles srovnatelné.