2. Jak vytrhnout ubrus zpod svatební hostiny

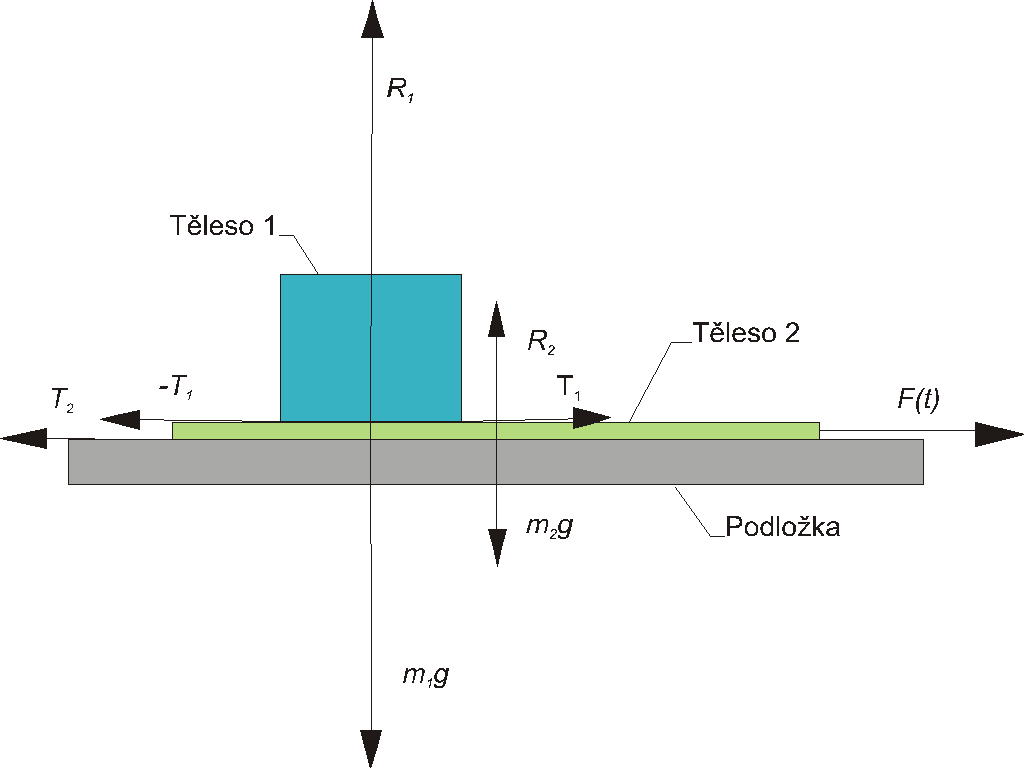
Tento název kapitoly je velmi nadnesený, nebudeme se zde snažit odhalit tajemství různých "fíglů" jak toto zvládnout, ale ukážeme zde velmi podrobně, jak za pomoci přiměřeného modelu a výpočetní techniky objasnit jevy spojené s pokusem "vytržení listu papíru zpod vázy", zobrazeném na obr.2.1. Těleso 1 představuje vázu, těleso 2 papír.

obr.2.1

…síla, jíž působíme na těleso 2, její časový průběh je zadán.

…třecí síla jíž působí těleso 2 na těleso1

…třecí síla jíž působí těleso 1 na těleso 2

…třecí síla, jíž působí podložka na soustavu těles 1+2 (resp. na těleso 2)

…tlaková síla, jíž působí těleso 2 na těleso 1

…výslednice tlakových sil, jimiž působí na těleso 2 podložka a těleso 1

Koeficient statického (resp. dynamického) tření mezi tělesy 1 a 2 je f_s1 (resp. f_d1), odpovídající koeficienty mezi tělesem 2 a podložkou jsou f_s2 (resp. f_d2).

Pro naše úvahy zvolíme takový model, že síla, jíž táhneme za list papíru, roste lineárně s časem, tedy F(t) = A.t (viz. graf.2.1 pro A=50).

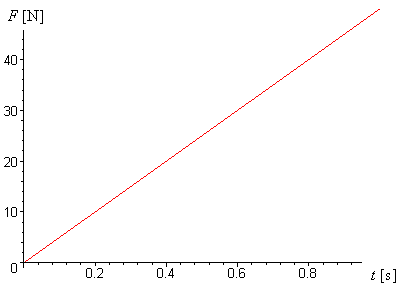
graf.2.1

Tělesa 1 a 2 se budou pohybovat pouze ve směru osy x (vazební podmínka), svislé složky sil působících na jednotlivá tělesa jsou tedy kompenzovány. Začnou-li se tělesa pohybovat vůči sobě, změní se statické tření na dynamické . V našem modelu se toto bude dít skokově.

Z obr.2.1 je vidět, jak budou vypadat pohybové rovnice pro těleso 1 a 2.

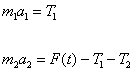(2.1)

Pohyb této soustavy těles budeme sledovat ve třech časových intervalech.

1. < 0 , t₁ ) Tělesa se nepohybují.
2. < t₁ , t₂ > Tělesa se pohybují společně (těleso 1 se nepohybuje vůči tělesu 2).
3. ( t₂ , infinity) Tělesa se pohybují jak vůči sobě tak vůči podložce.

Nyní se budeme postupně věnovat jednotlivým intervalům.

1. Tento interval označíme jako interval 1. Tělesa se nepohybují. Tahová síla působící na papír je tedy zřejmě kompenzována statickou silou třecí opačného směru a stejného časového průběhu, jíž působí podložka na soustavu těles 1 a 2 Síly a

jsou nulové, tj.:

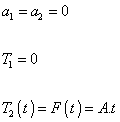
Určení okamžiku t₁:

V intervalu < 0 , t₁ ) platí pro velikost třecí síly vztah až do okamžiku t₁, kdy T₂ nabude nejvyšší přípustné hodnoty statické třecí síly určené koeficientem statického tření f_s2. Pak:

(2.2)

2. Tento interval označíme jako interval 2. Zde se pohybuje papír (těleso 2) společně s vázou (těleso 1). Je již překonána hranice statického tření mezi podložkou a papírem, tedy se již uplatňuje tření dynamické. Ovšem mezi vázou a papírem je tření stále ještě statické.

Pohybová rovnice vychází ze soustavy rovnic (2.1) pro tento časový interval takto:

, (2.3a)

kde a je společná hodnota veličin a₁, a₂.

(2.3b)

Tělesa se pohybují společně, tedy platí:

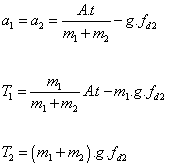
Určení okamžiku t₂ , kdy se začne pohybovat těleso 1 vůči tělesu 2:

Okamžiku t₂ odpovídá situace, kdy velikost statické třecí síly T₁ nabude maximální hodnoty dané koeficientem statického tření f_s1, tj.:

(2.4)

3. Tento označíme jako interval 3. Zde již dojde k pohybu obou těles soustavy vzhledem k podložce a zároveň i k vzájemnému pohybu těles 1 a 2.

V tomto intervalu budou pohybové rovnice pro soustavu těles 1 a 2 již shodné s tvarem (2.1), tj. po přepisu do diferenciálního tvaru a vyjádření jednotlivých sil získáme tvar:

(2.5a)

(2.5b)

Stanovili jsme okrajové body intervalů a mohli bychom přistoupit ke konkrétním výpočtům. K tomuto však potřebujeme zjistit, zda a za jakých podmínek probíhá experiment tak, jak jsme předpokládali, tj. okamžik t₂ následuje po t₁ (resp. je totožný s t₁). Zde se tedy naše úloha dělí na dvě části:

a) t₂ > t₁

Ze vztahů (2.2) a (2.4) vidíme, že okamžik t₂ následuje po t₁ , když platí:

f_s1 + f_d2 > f_s2 (2.6)

b) t₂ = t₁

Ze vztahů (2.2) a (2.4) vidíme, že okamžik t₂ je shodný s t₁ , když platí:

(2.7)

Nyní již můžeme přistoupit ke konkrétním výpočtům.

a) t₁ < t₂

Hned na začátku můžeme určit průběh třecích sil a výsledné síly působící na těleso 2 (). Použili jsme zde hodnoty reálného experimentu (parametry.2.1 , viz. str.17)

Graf závislosti velikosti třecí síly T₁ na čase (v itervalu <0;0.04> s je T₁ = 0).

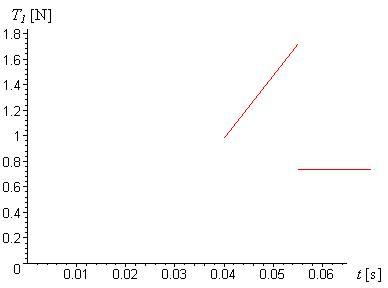
graf.2.2

Graf závislosti velikosti třecí síly T₂ na čase.

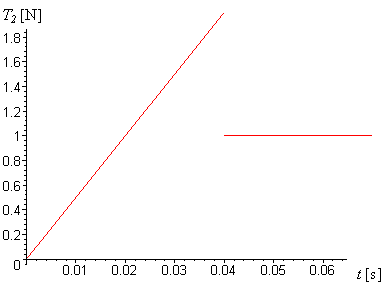
graf.2.3

Jak je vidět z grafu 2.4 v závislosti této síly na čase v okamžicích t₁ a t₂ jsou výrazné skoky, související se změnami statického tření na dynamické (v itervalu <0;0.04> s je F₂ = 0).

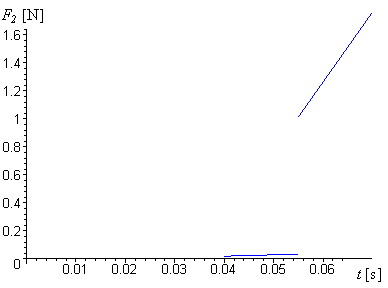
graf.2.4

První interval:

Pro interval 1 jsme již stanovili, že se tělesa 1 ani 2 nepohybují vůči podložce ani vůči sobě.

Druhý interval:

Pohyb těles zde popisují rovnice (2.2) v časovém intervalu < t₁ ; t₂ >. Jejím řešením dostaneme časovou závislost společné polohy těles 1 a 2 vůči podložce na čase:

(2.8)

Časovou závislost získáme i pro rychlost:

(2.9)

Závislosti (2.8) a (2.9) jsou výstupem z programu Maple pro zadané počáteční podmínky.

Třetí interval:

Pohyb těles zde popisuje soustava rovnic (2.5) v časovém intervalu ( t₂ ; infinity ). Její řešení určuje časovou závislost polohy jednotlivých těles vůči podložce. Na tomto místě uvedeme pouze obecné řešení soustavy rovnic (2.5) , partikulární řešení s použitím pouze proměnných vstupujících do výpočtu uvádět nebudeme, protože je příliš nepřehledné ,ale později si uvedeme toto řešení pro konkrétní případ, kde použijeme číselné konstanty.

Obecné řešení (2.5):

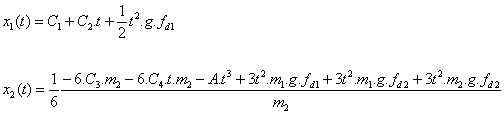(2.10)

Nyní ukážeme jak by vypadalo řešení pro konkrétní případ, kde je samozřejmě nutné uvést všechny parametry, které do výpočtu vstupují a mají samozřejmě význam i pro provedení případného experimentu.

Vstupní parametry (parametry.2.1):

g = 9,81 m.s^-2

m₁ = 0,50 kg

m₂ = 0,01 kg

A = 50

f_s1 = 0,35

f_s2 = 0,40

f_d1 = 0,15

f_d2 = 0,20

Kde A - konstanta úměrnosti ; g - tíhové zrychlení ; m₁ , m₂ - hmotnosti těles 1 a 2 ; f_s1 , f_d1 - koeficienty statického a dynamického tření mezi tělesem 1 a tělesem 2 ; f_s2 , f_d2 - koeficienty statického a dynamického tření mezi tělesem 2 a podložkou.

Jestliže budeme považovat počáteční stav soustavy za takový, že všechna její tělesa mají nulové polohy a rychlosti, pak můžeme řešení uvést v tomto tvaru:

V intervalu 1 nedochází k žádnému pohybu.

V intervalu 2 je závislost polohy na čase tato:

(2.11)

Závislost rychlosti na čase:

(2.12)

V intervalu 3 jsou závislosti poloh a rychlostí tyto:

Polohy:

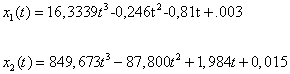(2.13)

Známe-li nyní závislosti poloh a rychlostí těles, můžeme je znázornit i graficky.

Graf závislosti poloh těles 1 a 2 na čase vůči podložce:

(získáme zkombinováním funkčních závislostí (2.11) a (2.13) v odpovídajících intervalech)

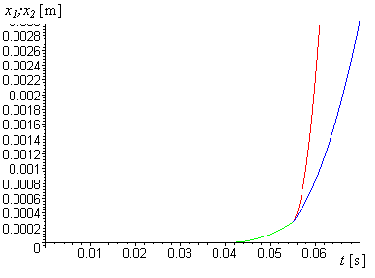
graf.2.5

Rychlosti:

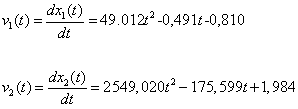(2.14)

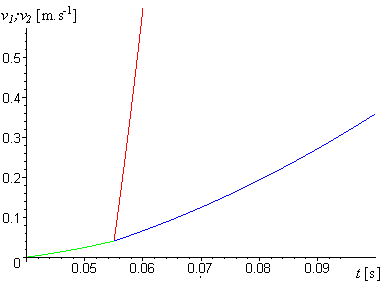
Graf závislosti rychlostí na čase vůči podložce:

(získáme zkombinováním funkčních závislostí (2.12) a (2.14) v odpovídajících intervalech)

graf.2.6

Zelená křivka vyjadřuje společný pohyb těles 1 a 2 , modrá křivka vyjadřuje pohyb tělesa 1 (vázy) od okamžiku t₂ , červená křivka vyjadřuje pohyb tělesa 2 (papíru) od téhož okamžiku.

Nespojitost v okamžiku t₂ mezi zelenou a modrou křivkou není příliš patrná, ale pokud bychom vypočetli hodnoty prvních derivací podle času zelené a modré křivky v bodě t₂, zjistili bychom, že v tomto bodě se funkce jak souřadnice, tak rychlosti mění skokem (tj. derivace se nerovnají).

b) t₁ = t₂

Situace se na rozdíl od předchozího změní tak, že vypadne druhý interval, tj. . Má tedy smysl uvažovat pouze o dějích v třetím intervalu.

Pro to aby splynuly okamžiky t₁ a t₂ musí být splněna podmínka (2.7), například zadáním těchto vstupních parametrů (parametry.2.2):

g = 9,81 m.s^-2

m₁ = 0,50 kg

m₂ = 0,01 kg

A = 50

f_s1 = 0,35

f_s2 = 0,55

f_d1 = 0,15

f_d2 = 0,20

Průběhy třecích sil T₁ a T₂ budou shodné s případem a), až na směrnice a okamžik přechodu ze statického na dynamické tření ( použijeme parametry.2.2 ).

V tomto případě je v grafu závislosti celkové síly F₂ působící na těleso 2 pouze jeden skok.

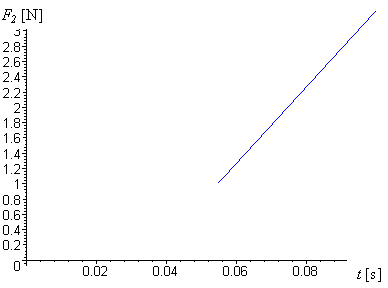
graf.2.7

Závislosti poloh a rychlostí v závislosti na čase těles 1 a 2:

Polohy:

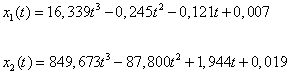(2.15)

Graf závislosti poloh v závislosti na čase těles 1 a 2:

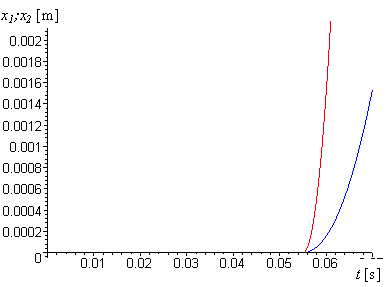
graf.2.8

Rychlosti:

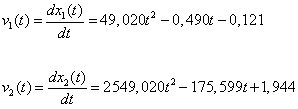
Graf závislosti rychlostí v závislosti na čase těles 1 a 2:

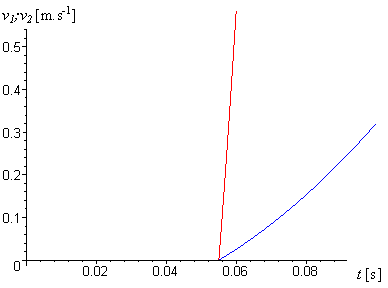
graf.2.9

Jak si zajisté pozorný čtenář všimnul neuvažujeme děje, které by nastaly v momentě, kdy těleso 1 (váza) dospěje na konec podložky a začne se z ní sesouvat, což v našem modelu znamená, že jak podložka, tak i těleso 2 (papír) jsou nekonečné části rovnoběžných polorovin. V tomto momentu by se tato úloha rozvětvila do několika dalších částí podle toho, jak by se těleso 1 chovalo v částečném kontaktu s tělesem 2 a podložkou. Tato situace by však pro běžného čtenáře byla příliš nepřehledná a překročila by rámec jevů, které jsme chtěli objasnit.