Goniometrie je nauka o měření úhlů. Existuje mnoho jednotek, ve kterých se měří úhly, např. stupně, grady, aj. Přirozeně je ovšem měříme v radiánech. Nechť je zadán úhel \(\angle AOB\) v rovině (\(|AO|=|BO|\)) a nakresleme kružnici o poloměru \(|AO|=|BO|\) se středem v bodě \(O\). Potom poměr délky orientovaného oblouku \(AB\) a poloměru \(|AO|\) nezáleží na volbě poloměru a délkových jednotek, ve kterých měříme, a říkáme mu velikost úhlu \(\angle AOB\).
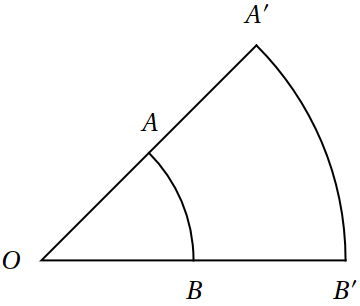
Velikost plného úhlu je \(2\pi\), jedná se o poměr obvodu kružnice a jejího poloměru.
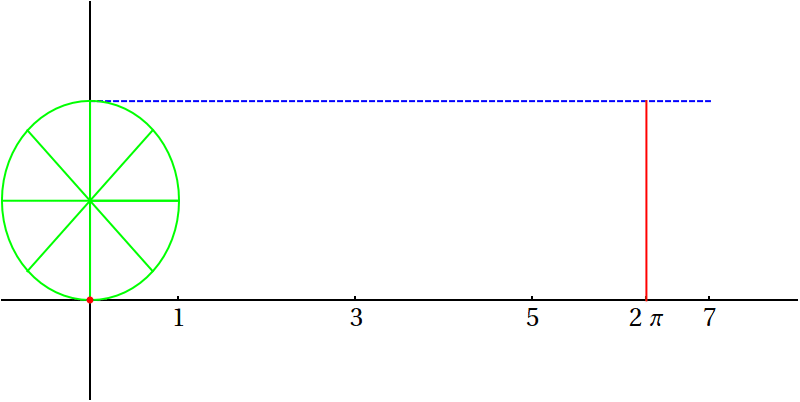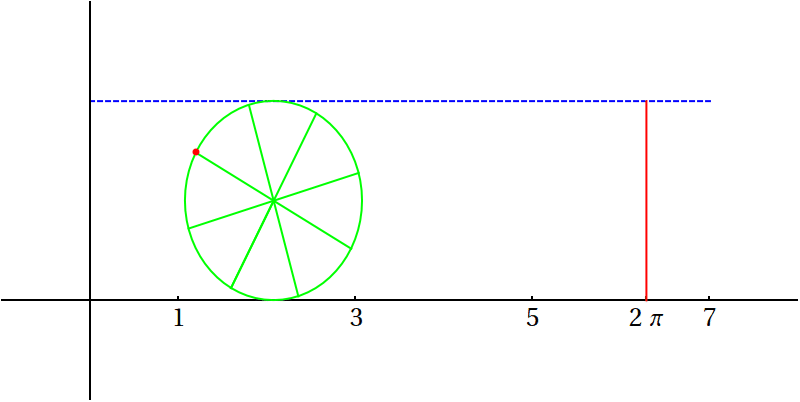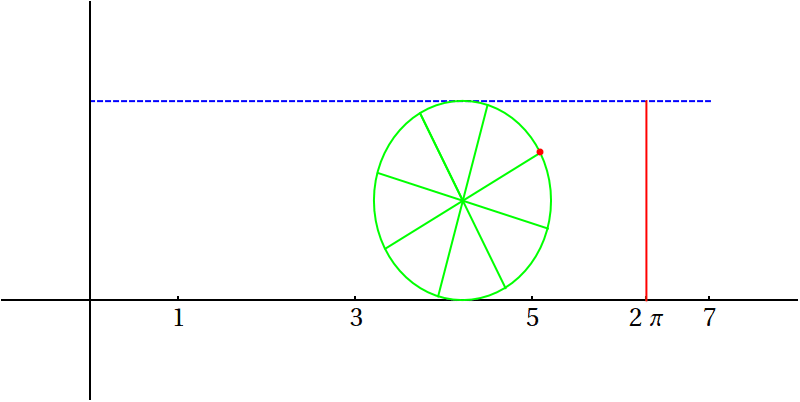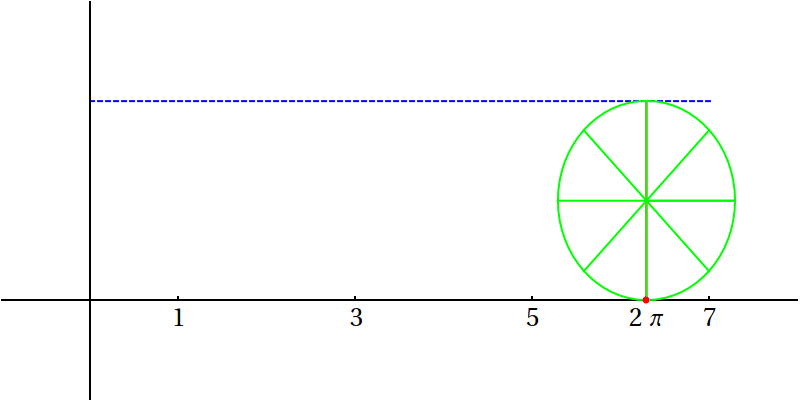
Číslo \(\pi\) představuje jednu z nejdůležitějších univerzálních matematických kontant a je přibližně známo od starověku. Více informací najdete na Wikipedii u hesla \(\pi\).
Základními objekty, z nichž lze poskládat všechny ostatní mnohoúhelníky, jsou trojúhelníky. Mnohoúhelníkem myslíme rovinný obrazec omezený konečným uzavřeným řetězcem orientovaných úseček: koncový bod jedné je počátečním bodem následující a koncový bod poslední je počátečním bodem první, přičemž žádné jiné body úseček nesplývají. Základním druhem trojúhelníku, pomocí něhož lze získat i ostatní obecné trojůhelníky, je trojúhelník pravoúhlý. K obecným trojúhelníkům se vrátíme později, až budeme vědět více o pravoůhlých trojůhelnících.
Zvláštním případem trojúhelníku je trojúhelník pravoúhlý, ve kterém alespoň jeden úhel (bez újmy na obecnosti \(\gamma\) je pravý, tj. \(\gamma = \pi/2\). Stranu proti pravému úhlu značíme obvykle \(c\) a nazýváme ji přeponou, zbylé strany nazýváme odvěsnami (značíme \(a\) a \(b\)). Jednoduše spočteme obsah pravoúhlého trojúhelníka jako \[ S = \frac{ab}{2}. \] Důležité tvrzení, které platí je
V pravoúhlém trojúhelníku je součet kvadrátů velikostí odvěsen roven kvadrátu velikosti přepony; s dříve zavedeným označením je \[ a^2 + b^2 = c^2. \]
Uvažme následující obrázek
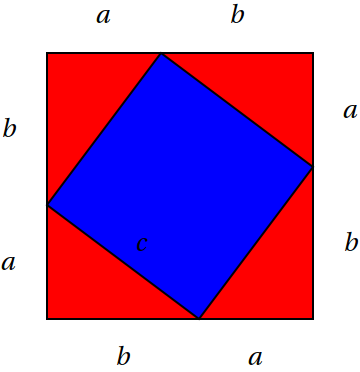
Potom obsah velkého čtverce na jedné straně získáme jako součet obsahu modrého čtverce a čtyř (až na otočení) shodných trojúhelníků, na druhé straně přímo. Je tedy \[ c^2 + 4 \frac{ab}{2} = (a+b)^2 = a^2 +2ab+b^2, \] odkud po vykrácení dostaneme dokazované tvrzení.
Předchozí konstrukce nám snadno dává i opačné tvrzení: pro každou trojici čísel \(a,b,c\) splňující \(a^2+b^2=c^2\) existuje pravoúhlý trojúhelník s přeponou o velikosti \(c\) a odvěsnami o velikostech \(a\) a \(b\).
Z předchozího tvrzení snadno zjistíme, že pravoúhlé trojúhelníky existují a je jich nekonečně mnoho. Uveďme se například některé trojúhelníky, jejichž délky stran jsou v nějakých jednotkách přirozená čísla.
| \(a\) | \(b\) | \(c\) |
| \(3\) | \(4\) | \(5\) |
| \(6\) | \(8\) | \(10\) |
| \(9\) | \(12\) | \(15\) |
Ve skutečnosti je nekonečně mnoho i takových pythagorejských trojic, jež nejsou svými násobky, jako např. \((6,8,10)=2(3,4,5)\).
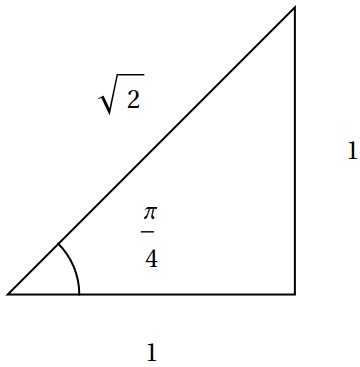
Dále připomínám trojúhelníky, jež jsou speciální. Prvním je rovnoramenný pravoúhlý trojúhelník.
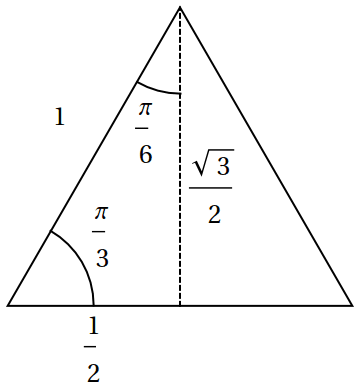
Dalším speciálním případem je rovnostranný trojúhelník, který sice není pravoúhlý, ale obsahuje dva zrcadlově převrácené pravoúhlé trojúhelníky.
(Pravoúhlý) trojúhelník má tři strany a poměr je podíl dvou čísel. Počet různých dvojic tvořených třemi stranami je dán kombinačním číslem \( {3\choose 2} = 6 \), je tedy \(6\) různých trigonometrických funkcí, dvě z nich se ale užívají jen zřídka.
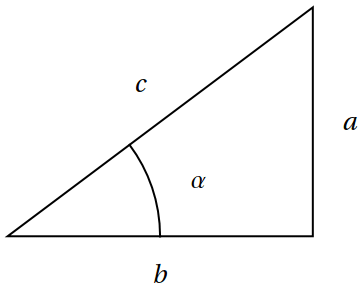
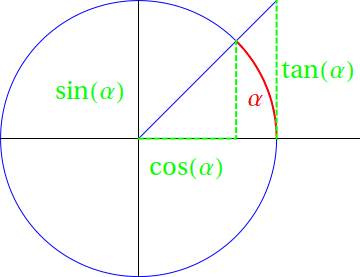
V obecném pravoúhlém trojúhelníku, jehož úhel proti straně \(a\) je \(\alpha\) definujeme sinus \(\alpha\), zkráceně \[ \sin \alpha = \frac{a}{c} \] jako poměr délky protilehlé odvěsny a přepony. Převrácený poměr se používá řídce a nazývá se kosekans.
Dále definujeme kosinus \(\alpha\), zkráceně \[ \cos \alpha = \frac{b}{c} \] jako poměr délky přilehlé odvěsny a přepony. Převrácený poměr se používá řídce a nazývá se sekans.
Poslední důležitá dvojice poměrů je tangens \(\alpha\) a kotangens \(\alpha\), zkráceně \[ \tan \alpha = \frac{a}{b}, \quad\quad \cot \alpha = \frac{b}{a}. \]
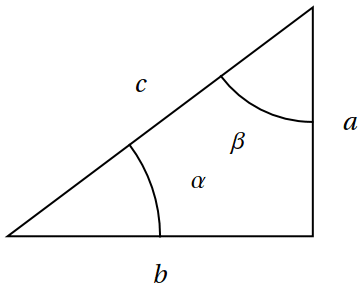
Pro \(\alpha+\beta=\frac{\pi}{2}\) platí \(\sin\alpha=\cos\beta\) a \(\cos\alpha=\sin\beta\) se značením z předchozího obrázku.
Při záměně \(\alpha\) za \(\beta\) se zamění protilehlá a přilehlá odvěsna.
S předchozím značením platí \(\sin^2\alpha+\cos^2\alpha = 1\).
Jedná se o přímý důsledek Pythagorovy věty. \[ \begin{align} a^2 + b^2 &= c^2 \\ \left(\frac{a}{c}\right)^2 + \left(\frac{b}{c}\right)^2 &= 1 \\ \sin^2\alpha+\cos^2\alpha &= 1. \end{align} \]
| \(x\) | \(\sin\alpha\) | \(\cos\alpha\) | \(\tan\alpha\) | \(\cot\alpha\) |
| \(\sin\alpha\) | \(x\) | \(\sqrt{1-x^2}\) | \(\frac{x}{\sqrt{1-x^2}}\) | \(\frac{\sqrt{1-x^2}}{x}\) |
| \(\cos\alpha\) | \(x\) | |||
| \(\tan\alpha\) | \(x\) | |||
| \(\cot\alpha\) | \(x\) |
Dokážeme dále zajímavé tvrzení i jeho opačnou implikaci.
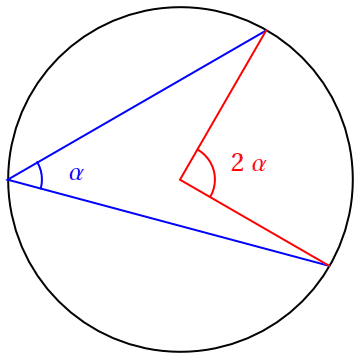
Velikost úhlu vepsaného kružnici je polovinou velikosti patřičného obloukového úhlu.
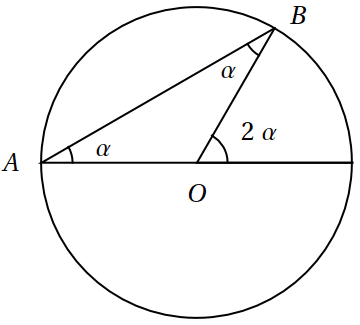
Napřed dokážeme tvrzení pro jednodušší situaci, kdy jedno rameno vepsaného úhlu prochází středem kružnice. Součet úhlů v trojúhelníku dává \(\pi\), tedy \(\angle AOB = \pi-2\alpha\). Ale hledaný obloukový úhel je k němu doplňkový do \(\pi\). Dále vyřešíme situaci, kdy úsečka spojující vrchol vepsaného úhlu a střed kružnice leží uvnitř vepsaného úhlu. Tuto situaci lze vyřešit dvojnásobnou aplikací již dokázaného tvrzení pro jednodušší situaci. Zbývající možnost lze řešit obdobně.
Velice jednoduchým důsledkem předchozí věty je tzv. Thaletova věta. Formulujte ji a pomocí předchozí věty ji dokažte. Opět také platí i opačné tvrzení, je zde ovšem menší komplikace.
Značení v trojúhelníku ponecháme standardní, vrcholy \(A,B,C\), u nich příslušné úhly \(\alpha,\beta,\gamma\) a naproti nim strany \(a,b,c\).
Platí \(\frac{a}{\sin\alpha}= \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}\).
Vyjádříme všechny tři výšky v trojúhelníku a to vždy dvěma způsoby. \[ \begin{align} v_c &= a\sin\beta = b\sin\alpha \\ v_a &= b\sin\gamma = c\sin\beta \\ v_b &= c\sin\alpha = a\sin\gamma. \end{align} \] Odtud již přímo dostáváme požadovaný vztah.
Platí \(c^2 = a^2+b^2-2ab\cos\gamma\).
Stranu \(a\) rozděluje výška \(v_a\) na dvě úsečky délky \(p\) a \(q\) a celý trojúhelník zase rozdělí na dva pravoúhlé trojúhelníky. Aplikací Pythagorovy věty na oba dva dostáváme \[ c^2 = v_a^2+p^2 = b^2-q^2+p^2 = b^2-q^2+(a-q)^2=a^2+b^2-2aq=a^2+b^2-2ab\cos\gamma, \] což jsme chtěli ukázat.
Orientovanému úhlu můžeme přiřadit jeho sinus, kosinus, tangens, kotangens, atd. Takovému přiřazení říkáme (reálná) funkce (reálné) proměnné. Názorně můžeme zobrazit pro danou hodnotu úhlu goniometrické funkce pomocí jednotkové kružnice v rovině se středem v počátku.

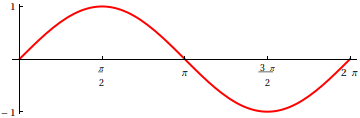
Ještě jednou se podívejme na podrobnější statický graf funkce sinus.
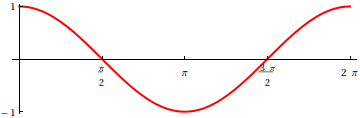
Obdobně bychom vytvořili graf funkce kosinus, vzhledem k dokázané větě o doplňkových úhlech je graf jen posunutý o \(\pi/2\) a zrcadlený vzhledem k horizontální ose.
Ještě jednou se podívejme na podrobnější statický graf funkce tangens.
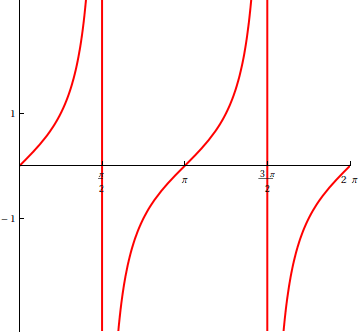
Inverzní goniometrické funkce arkussinus, arkuskosinus a arkustangens definujeme standardně jako inverzní funkce s patřičně omezeným oborem hodnot: pro arkussinus a arkustangens je to \([-\pi/2,\pi/2]\), pro arkuskosinus \([0,\pi]\). Definiční obory sinu a kosinu jsou \([-1,1]\), tangensu \((-\infty,\infty)\). Grafy těchto funkcí jsou zřejmé z grafů sinu, kosinu a tangensu.