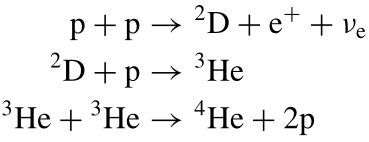
Podzim 2020
Termín plazma byl zaveden v polovině 19. století českým fyziologem Janem Evangelistou Purkyně. Popisuje tekutinu, která zbude z krve poté, co se z ní oddělí krevní buňky.
Ve dvacátých letech 20. století americký fyzik Irving Langmuir začal používat termín plazma pro popis ionizovaného plynu obsahujícího:
Co ho k tomu vedlo nevíme. Nicméně, poté co z ionizovaného plynu odstraníme všechny nabité částice tak nám zbude pouze neutrální plyn, tedy nic pro co by se dal použít termín plazma, protože neutrální plyn bez nabitých částic ztratí všechny vlastnosti plazmatu.
Navíc, od té doby fyzikové plazmatu, musejí neustále vysvětlovat nezasvěcenému zbytku lidstva, že vlastně nestudují krev.
Protože čeština je důmyslný jazyk, v případě, že mluvíme o krevní plazmě, jedná se o tu plazmu. Zatím co, v případě fyzikálních souvislostí, se jedná o to plazma. Mluvíme tedy o fyzice plazmatu, ale o dárcích krevní plazmy.
Plazma ve Sluneční soustavě
Jaderné reakce v nitru Slunce
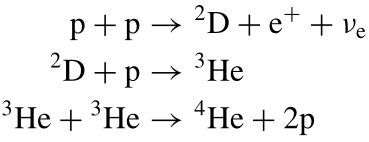
Proton protonový cyklus: 26.21MeV se uvolní ve formě tepla, 0.51MeV odnese neutrino.
Sluneční korona

Korónové smyčky naplněné horkým plazmatem, které září v oblasti měkkých rentgenových paprsků. Pozorováno na vlnové délce 17.1 nm satelitem pro průzkum přechodové oblasti a koróny (TRACE). (Credits: NASA/TRACE)
Sluneční erupce
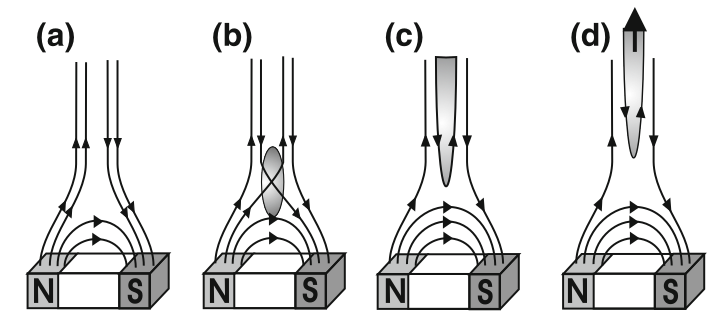
Vývoj sluneční erupce podle modelu Sweet-Parker:.
Dipólové pole korónové smyčky je spojeno s meziplanetárním magnetickým polem.
Propojením antiparalelních magnetických čar se uvolní napětí magnetických čar.
a d) Uvolňující se magnetické pole zrychluje zachycené plazma. (credits: Piel)
Sluneční vítr
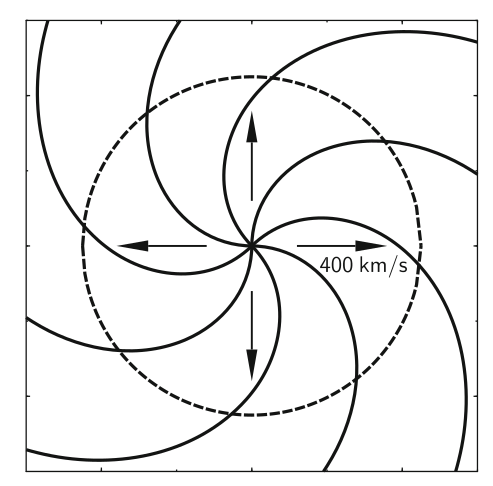
Rotace slunce tvaruje paprsky slunečního větru, které vycházejí z určitých míst, do Archimédovy spirály.
Interakce slunečního větru s magnetickým polem Země
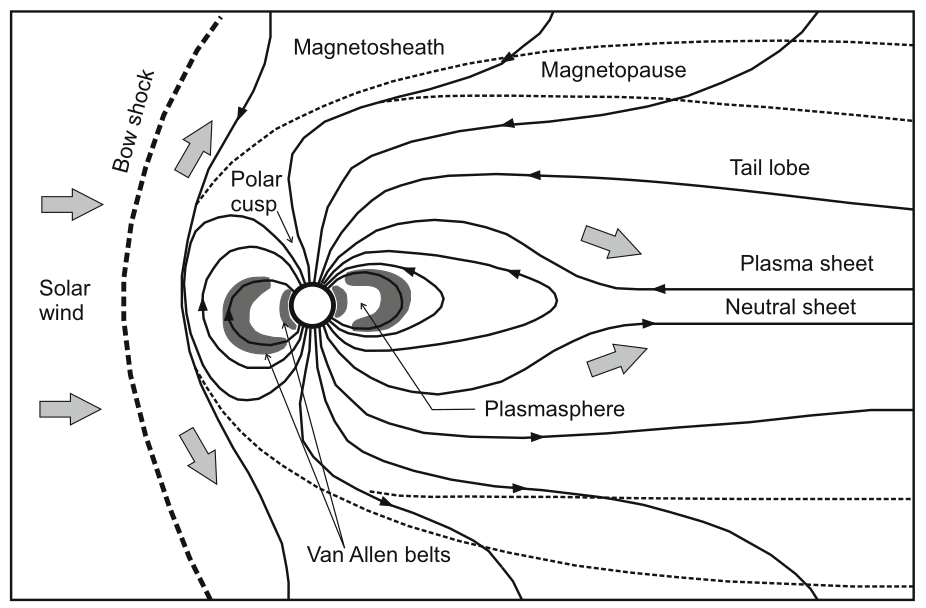
van Allenovy radiační pásy
Dipólové magnetické pole Země zachycuje energetické nabité částice. Částice v něm gyrují, bouncují a driftují a vytvářejí prstencový proud. Oblasti zvýšené koncentrace těchto částic v okolí Země se nazývají van Allenovy radiační pásy.
Byly objeveny při analýze dat z Geigerových—Muellerových čítačů, které byly umístěné na prvních amerických satelitech (Explorer 1 a Pioneer 3, r. 1958). Čítače měly za úkol měřit tok kosmického záření ze vzdálenho vesmíru (zdroje mimo naši sluneční soustavu). Cílem bylo zjistit jaký je tok kosmického záření ve vesmíru v porovnání s tokem měřeným na Zemi.
Zjištěný tok energetických částic ve vesmíru, tak drasticky převýšil očekávané hodnoty (čítač úplně zahltil), že van Allenovy spolupracovníci to komentovali slovy: ‘My God, space is radioactive!!’ Brzy poté přišla myšlenka že měřený tok energetických částic jsou částice zachycené v magnetickém poli Země a ne kosmické záření přicházející ze vzdáleného vesmíru.
Vnitřní pás je lokalizován zhruba ve vzdálenosti 1.6 násobek poloměru Země. Vnější radiační pás je ve výšce zhruba 4 násobek poloměru země. Ve vzdálenosti 2.2 \(R_{e}\) je mezera, kde radiační efekty jsou minimální. Orbity GPS satelitů jsou práve v této mezeře.
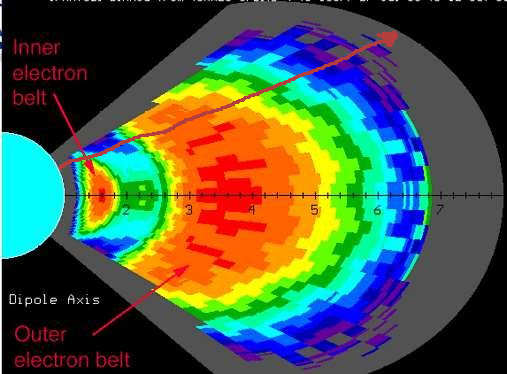
Při cestě člověka k Měsíci je nutné plánovat průlet van Allenovými pásy takovým způsobem, aby pro posádku byla absorbovaná dávka ionizujícího záření co nejmenší. Při průletu podél naznačené trajektorie bude čas strávený v oblastech zvýšeného záření zhruba hodina (při cestovní rychlosti kolem 25000 km/hod). Absorbovaná dávka pak bude kolem 16 Rad (letální dávka absorbovaného záření je kolem 300 Rads za hodinu). Dozimetry astronautů cestujících k Měsíci a zpět ukázaky méně než 2 Rad. Hodnota 16 Rad by byla při průletu radiačními pásy naznačenou trajektorií je pro astronauta nechráněného kosmickou lodí.
Ionosféra Země
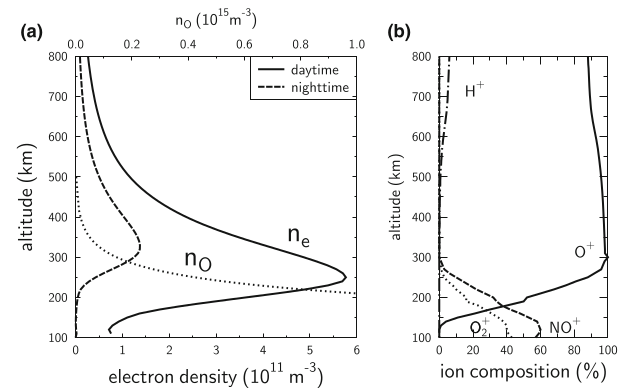
Plasma v atmosféře
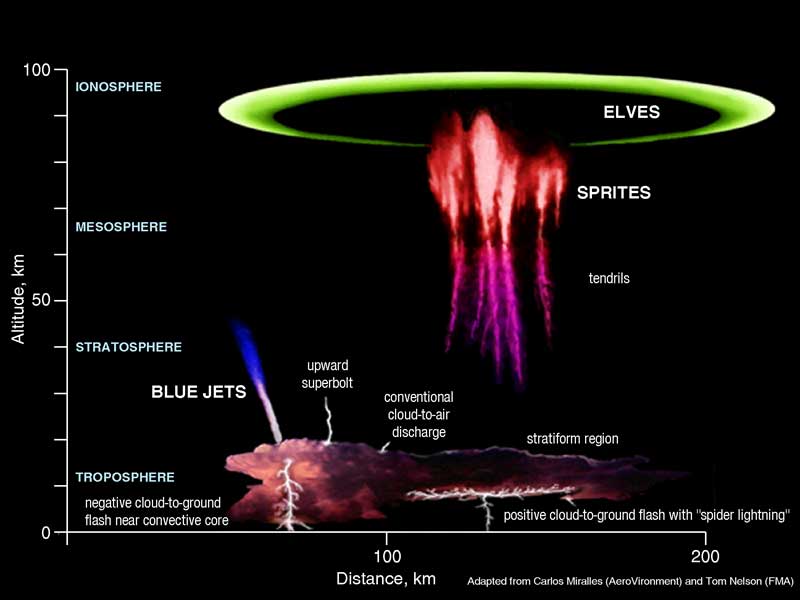
Definice:
Plazma je kvazineutralní plyn složený z kladně a záporně nabitých částic, který vykazuje kolektivní chování.
Záporně nabité částice jsou obvykle elektrony, kladné jsou ionty. V elektronegativních plynech se mohou vyskytovat i záporně nabité ionty vzniklé navázáním elektronu na neutrální atom nebo molekulu. Přítomnost neutrálních částic v plazmatu je častá, hlavně v pozemských plazmatech.
Definice plazmatu obsahuje dva pojmy, které je nutné vysvětlit:
Kvazineutrální: znamená, že v makroskopickém objemu je stejné množství kladných a záporných nábojů. Takový systém nabitých částic není zdrojem makroskopického elektrostatického pole.
Kolektivní chování: znamená že nabité částice v plazmatu se nechovají jako jednotlivé nezávislé částice. Každá nabitá částice v plazmatu interaguje s mnoha dalšími nabitými částicemi najednou. Kolektivní chování je důsledkem dalekodosahové Coulombovské interakce nabitých částic.
Na plazma je možné se dívat jako na čtvrté skupenství hmoty. Jednotlivá skupenství hmoty se liší poměrem kinetické energie náhodného pohybu částic hmoty (tepelné energie) a vazebné energie, která částice drží pohromadě.
\[ \frac{\hbox{kinetická energie náhodného pohybu}}{\hbox{vazebná energie}} \]
Převládá-li vazebná energie nad kinetickou, hmota je ve formě pevné látky. Přidáním energie do systému může dojít k překonání vazebných sil a látka může přejít do stavu který je charakterizován větší hodnotou daného poměru. Z pevné látky se stane kapalina, z kapaliny plyn. Jedná se změny skupenství (fázové přeměny).
Přidáváním další energie do systému bude docházet k disociaci molekul plynu, a k postupné ionizaci. Takový přechod se zvyšováním tepelné energie v plynu je pozvolný, charakterizovaný stupněm ionizace \[ \alpha = \frac{n_{\rm i}}{n_{\rm i}+n_{\rm n}}, \] kde \(n_{\rm i}\) je koncentrace iontů a \(n_{\rm n}\) je koncentrace neutrálů.
Stupeň ionizace je dán rovnováhou mezi ionizací, která vzniká v důsledku srážek částic s velkou energií a rekombinací. Rovnice popisující poměr ionizovaných atomů a neutrálů se nazývá Sahova rovnice \[ \frac{n_{\rm i}}{n_{\rm n}}=a \frac{T^{3/2}}{n_{\rm i}} \exp{\left(-U/k_{\rm b}T\right)}, \] pro plyn v rovnováze o teplotě \(T\) s ionizační energií U. Vliv rekombinace má na svědomí přítomnost \(n_{\rm i}\) ve jmenovateli. Konstanta \(a=2.405\times10^{21}\,m^{-3}K^{-3/2}\).
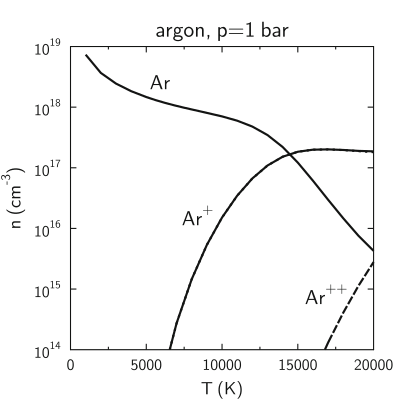
Příklad:(Principles… str. 72) Odhadněte stupeň
ionizace vzduchu za atmosferického tlaku a pokojové teploty (300K).
Výpočet opakujte pro teplotu 8000 K. Předpokládejte, že hlavní složkou
vzduchu je dusík s ionizačním potenciálem 14.5 eV.
[\(\alpha_{300K}=10^{-122}\), \(\alpha_{8000K}=0.0012\)].
Otázka: Jaký je maximální poloměr koule, která vznikne použije-li se celá tepelná energie částic v plazmatu na separaci náboje?
Předpokládáme nehybné ionty a elektrony o teplotě \(T\) a hustotě \(n_{\rm e}\) Tepelná energie v kouli o poloměru \(R\) je:
\[W_T = \frac{3}{2}n_{\rm e} k_{\rm b} T \cdot \frac{4}{3}\pi R^3\quad \hbox{(hustota tepelné energie $\cdot$ objem koule)}\]
Energie v elektrostatickém poli:
\[W=\int_{\rm (koule) }
\frac{1}{2}\varepsilon_0 E^2 {\rm d}V = \pi\frac{2n_{\rm
e}^2q^2}{4\pi\varepsilon_0}\] Elektrony utečou kam jim vznikající
elektrické pole dovolí. Jejich původní kinetická energie se přemění na
enegii elektrostatického pole.
Z rovnosti mezi \(W_T\) a \(W\) dostaneme poloměr \[R^2=45\frac{\varepsilon_0 k_{\rm b}T}{n_{\rm e}
q^2}, \quad R\sim 7 \lambda_D\] Tepelná energie elektronů jim
dovolí vytvořit oblast kde je porušená kvazineutralita. Charakteristická
délka na které porušení kvazineutrality plazmatu může nastat se nazývá
Debyeovská délka a je základní prostorovou škálou při popisu
plazmatu.
Debyeovská délka:
\[\lambda_{\rm D}^2 = \frac{\varepsilon_0
k_{\rm b}T}{n_{\rm e} q^2}. \]
Kvazineutralita plazmatu je důsledek toho, že nabité částice v plazmatu nemají dostatečnou tepelnou energii na to, aby se prostorový náboj mohl vyskytovat na vzdálenostech větších než je \(\lambda_{\rm D}\)
Schopnost plazmatu odstínit elektrostatické pole je jedna z jeho
základních vlastností. Vložíme-li do plazmatu testovací náboj \(Q\), v plazmatu kolem něj vznikne vrstva
náboje opačného znaménka, tak že v jisté vzdálenosti od náboje bude
elektrostatické pole tohoto náboje vykompenzováno oblakem opačného
náboje, který jej obklopuje. Tomuto procesu se říká
stínění. Charakteristický rozměr stínícího oblaku
(Debyeovská sféra) je \(\sim \lambda_{\rm
D}\). 
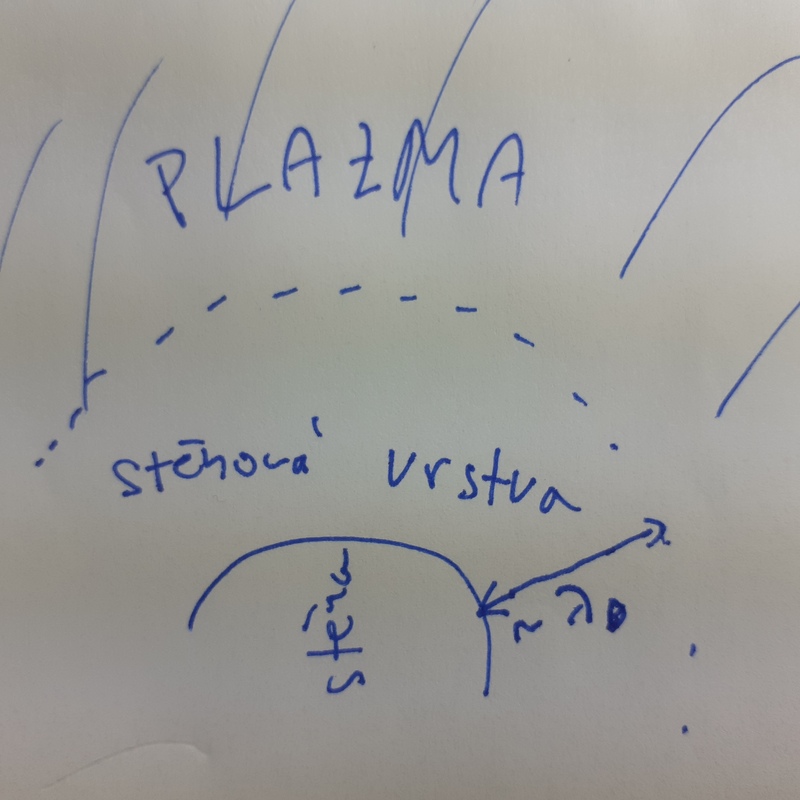
Stínění funguje nejen na náboje ale i v případě, že do plazmatu vložíme nějaký objekt. Kolem stěny objektu vznikne stěnová vrstva, neboli sheath. Kvazineutralita plazmatu je v sheathu narušena (prostorový náboj, převládá náboj jednoho znaménka). Velikost sheathu je opět, několikanásobek Debyeovské délky.
Uvažujme kvazineutrální plazma s koncentrací \(n=n_{\rm e}=n_i\). Vychýlením sloupce záporného náboje (elektronů) dojde s separaci náboje, kde na jedné straně vznikne přebytek kladného náboje a na druhé straně záporného. Tento prostorový náboj vytvoří elektrostatické pole, které působí vratnou silou na vychýlený náboj.
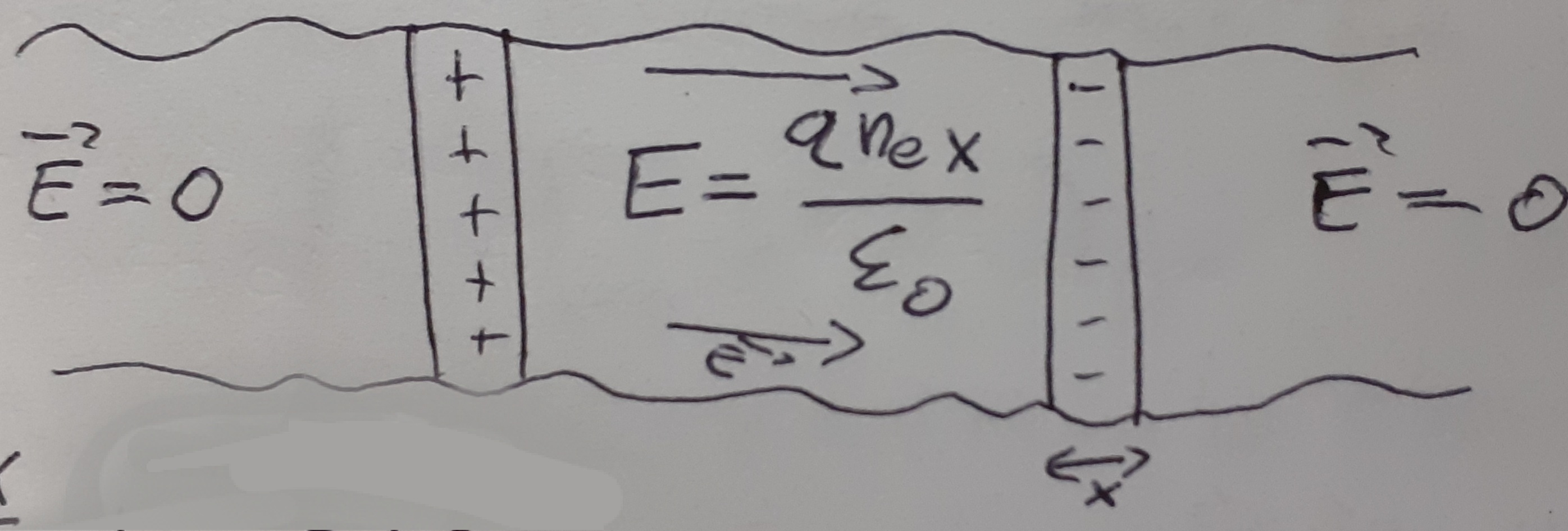
Pohybová rovnice popisující vychýlení náboje: \[ \frac{{\rm d}^2 x}{{\rm d} t^2} + \frac{n_{\rm e}q^2}{m_{\rm e}\varepsilon_0} x = 0 \] Jedná se o periodický pohyb ve kterém dochází k přelévání kinetické energie elektronů v potenciální energii elektrostatického pole. Vzniknou rychlé oscilace fluktuací v elektronové hustotě, kdy elektrony kolektivně kmitají kolem masivních iontů.
Plazmové oscilace mají Plazmovou frekvenci \[ \omega_{\rm pl}=\left(\frac{n_{\rm e}q^2}{m_{\rm e}\varepsilon_0}\right)^{1/2} \]
Oscilace takto fungují ve studeném bezsrážkovém plazmatu.
Důsledek: elektromagnetické vlny prochází plazmatem jen tehdy, je-li jejich frekvence větší než \(\omega_{\rm pl}\). Kovy jsou průhledné pro frekvence UV a vyšší…
Fyzický rozměr systému musí být velký v porovnání s \(\lambda_{\rm D}\): \[\begin{gather} L >> \lambda_{\rm D} \end{gather}\]
Stínění v plazmatu je důsledkem kolektivního chování částic v Debyeovské sféře, počet elektronů v Debyeovské sféře musí být velký: \[\begin{gather} N_D := \frac{4 \pi}{3} n \lambda_{\rm D}^3 >> 1 \end{gather}\]
Plazma musí být makroskopicky neutrální \[\begin{gather} n_{\rm e} = \sum n_{i} \end{gather}\]
Srážky neutrálů s elektrony (e-n srážky) tlumí kolektivní plazmové oscilace. Ionizovaný plyn bude plazmatem bude-li frekvence e-n srážek menší než plazmová frekvence \[\begin{gather} \nu_{\rm en} < \nu_{\rm pl} \quad (\hbox{kde } \nu_{\rm pl}=\omega_{\rm pl}/2\pi) \end{gather}\]
Uvážíme-li plasma s \(n_{\rm e}= 10^{10}\,\)m\(^{-3}\) a teplotou \(10^{3}\,\)K, které splňuje podmínku 1. až 3., pak bude-li koncentrace neutrálních částic \(n_n\) relativně nízká (například mezihvězdný plyn, kde \(n_{\rm e}>>n_{\rm n}\)), střední doba mezi e-n srážkami bude dlouhá ve srovnání s periodou plazmových oscilací a neovlivní kolektivní chování elektronů (plazma). Naopak bude-li \(n_n\) o mnoho řádů větší než \(n_{\rm e}\) kolektivní pohyb elektronů bude rušen srážkami s neutrály.
Plazmata pro která je \(N_D>1\) jsou slabě spřažená,
Plazmata pro která je \(N_D<1\) jsou silně spřažená.
Pro tepelná energie elektronů \(k_b T_e\) srovnatelnou nebo vyšší než je klidová hmotností elektronů \(m_e c^2\) mluvíme o relativistickém plazmatu.
Kvantové efekty začnou být v plazmatu důležité, bude-li střední vzdálenost částic srovnatelná s termální de-Brogliho vlnovou délkou \[ \lambda_{\rm dB} = \frac{h}{m_e v_{\rm th}} \sim n_e^{-1/3}, \] kde \[ v_{\rm th}=\sqrt{2k_b T_e/m_e} \] je nejpravděpodobnější rychlost v rovnovážném rozdělení rychlostí. Pro taková plazmata bude Pauliho vylučovací princip hrát podstatnou roli (Fermi-Diracova statistika). Mluvíme o kvantově degenerovaném plazmatu, které nalezneme ve vyhořelých hvězdách jako jsou např. bílí trpaslíci (vylučovací princip brání jejich finálnímu kolapsu).
Základními parametry plazmatu jsou
hustoty jednotlivých částic (koncentrace, number density) v jednotkách m\(^{-3}\).
Teplota jednotlivých složek plazmatu (elektrony, ionty, neutrály). Typicky se používá jednotka eV. 1eV ~11605 K (náboj elektronu / boltzmannova konstanta).
statické magnetické pole [T].
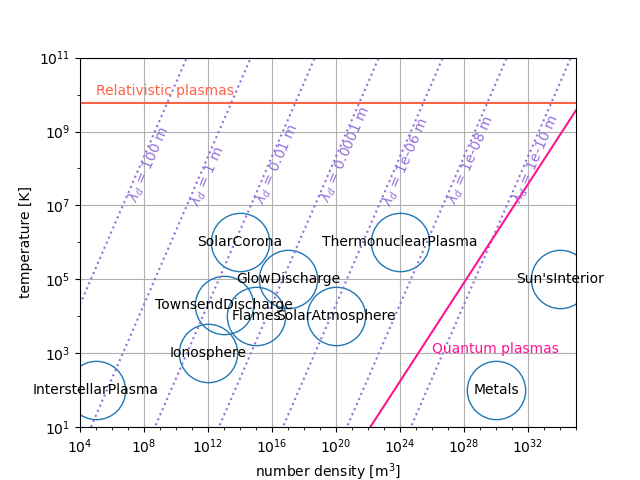
Pozemské nefúzní plazma:
\(T_{\rm e} \sim 10^0\,\)eV, teploty
iontů většinou nižší (\(10^{-2}\,\)eV).
hustota plazmatu \(10^{14}-10^{22}\)
m\(^{-3}\) (vzduch 1atm STP: \(2.7\times 10^{25}\,\) m\(^{-3}\) )
Pozemské fúzní plazma:
\(T_{\rm e} \sim 10^2-10^4\,\)eV,
Magnetické pole v řádu 1-10 T (zemské magnetické pole na povrchu: \(10^{-5}\))
magnetické udržení: hustota \(10^{19}-10^{22}\,\)m\(^{-3}\)
inerciální fúze: hustota \(10^{27}\,\)m\(^{-3}\)
Plasma ve vesmíru:
Mezihvězdný prostor: hustota \(10^{6}\,\)m\(^{-3}\)
Hvězdná atmosféra: hustota \(10^{20}\,\)m\(^{-3}\)
tyto plazmata jsou většinou planě ionizovaná, teploty elektronů v
rozmezí 1-100eV.
Plazmata jsou velice komplexní systémy, které jsou navíc velice vzdálené běžné intuici a každodenní zkušenosti. Vybudování potřebné intuice pro chování plazmatu vyžaduje značné úsilí.
Dobrá věc na plazmatu je, že je škálovatelné: podobné chování lze pozorovat v plazmatech, které se liší o mnoho řádů v hodnotách parametrů (\(n_{\rm e}\), \(T\), \(B\), …).
Fyzika plazmatu dává dokupy různé pohledy a přístupy na jednu věc. Typicky se snažíme popsat chování plazmatu z různých perspektiv a snažíme se tyto postupy logicky propojit.
Plazma se skládá z velkého počtu částic, elektronů, iontů, neutrálů.
Elektromagnetické pole působí na částice silou, a samy částice jsou zdrojem elektromagnetického pole. Popsat dynamiku takového systému vyžaduje tzv. selfkonzistentní přístup.
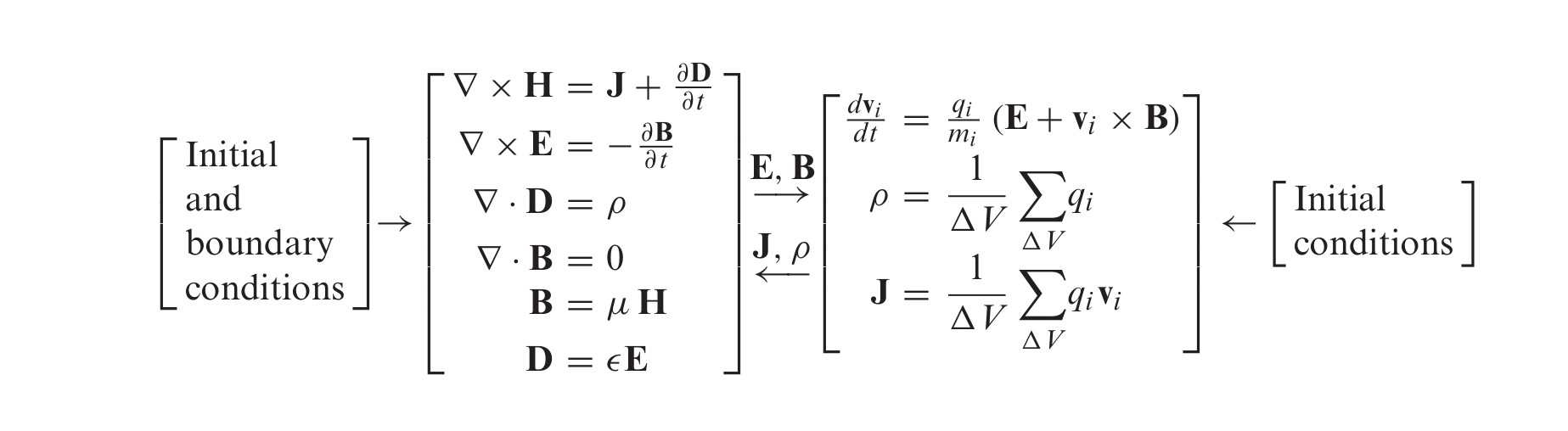
V principu lze časový vývoj plazmatu stanovit tak, že
v každém čase \(t\), ze známé polohy \({\bf x}(t)\) a rychlosti \({\bf v}(t)\) každé nabité částice a konfigurace vnějších \({\bf E}\) a \({\bf B}\) polí spočítáme řešením Maxwellových rovnic \({\bf E}\) a \({\bf B}\) pole v místech kde se nacházejí částice plazmatu.
sílu působící na každou částici \(j\) spočítáme užitím Lorentzovy rovnice \[ m_j {\bf a}_j = q_j({\bf E}({\bf x}) + {\bf v}_j \times {\bf B}({\bf x})) \] a jejím řešením pak stanovíme novou polohu a rychlost každé částice v čase \(t+\delta t\).
Cyklus pokračuje zase krokem 1.
Takový popis je koncepčně velice jednoduchý ale prakticky neproveditelný.
kvůli velkému počtu částic
kvůli složitosti elektromagnetických polí.
Jednotlivé jevy, které budeme v plazmatu studovat budeme nahlížet s odpovídajícím zjednodušením, které ovšem uchová potřebnou podstatu problému.
Situace popsaná příslušnou sadou aproximací, které poskytují potřebný selfkonzistentní popis systému se nazývá režim.
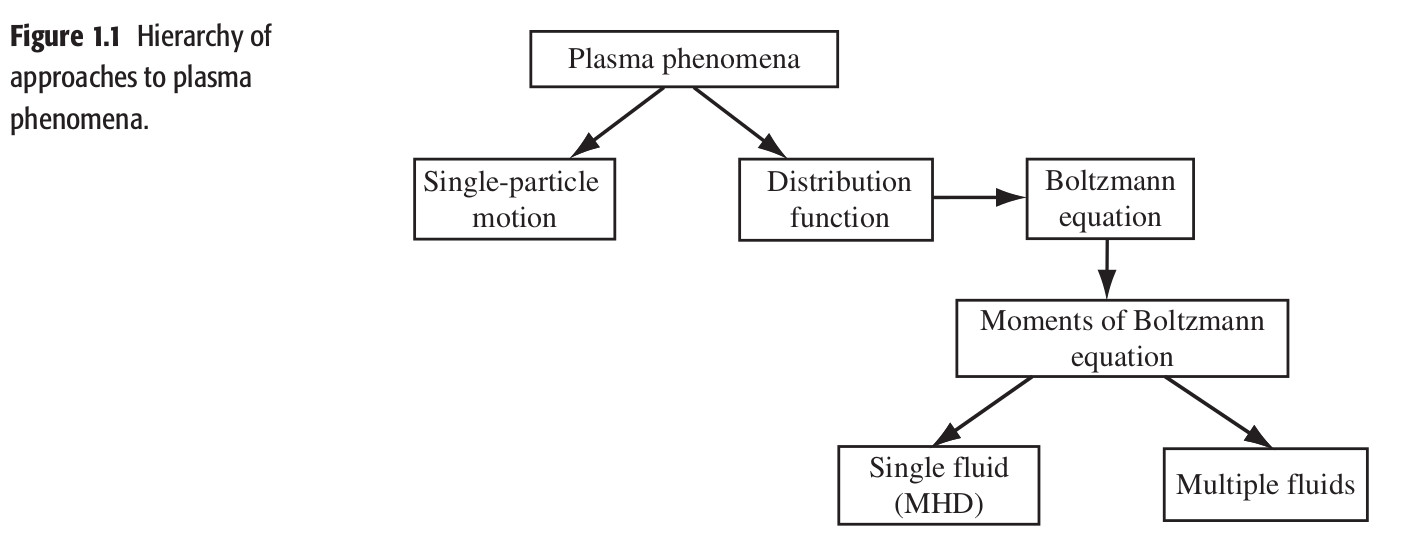

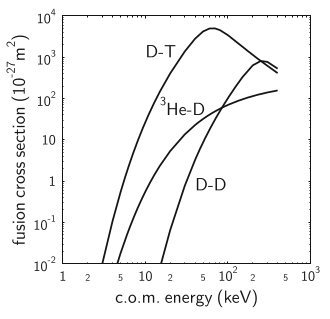
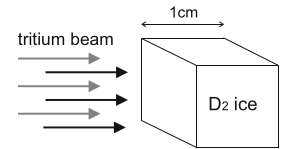
Proč ne?

ITER
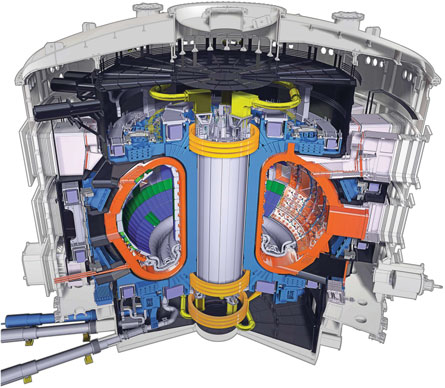
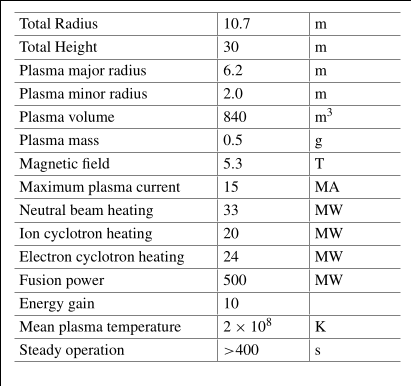
Wendelstein 7-X

“Nuclear fusion breakthrough: Scientists generate more power than used to create reaction” Tue, Dec 13 2022…(Lawrence Livermore National Laboratory)
“US scientists achieve net energy gain for second time in nuclear fusion reaction” Sun 30 Jul 2023
Plazmové technologie….
Iontové motory využívají paprsek iontů urychlených na
rychlosti v řádu desítek km/s. Plazma je zde médium ve kterém se nárazem
elektronů ionizuje neutrální plyn. Rychlost urychlených iontů je až
desetinásobná ve srovnání s chemickými raketami => na stejné \(\Delta v\) je potřeba mnohem menší hmotnost
paliva.
Vynést jeden 1 kg nákladu na oběžnou dráhu stojí kolem $20,000! První
iontový motor byl sestrojen v padesátých letech Haroldem R. Kaufmanem v
laboratořích NASA. První výzkumná mise, která použila iontové motory
byla sonda Dawn, start: 2007, studovala protoplanety Vesta a Ceres.
Iontový pohon jí umožnil vstoupit a vystoupit z gravitačního pole
několika těles. Sondy s konvenčním pohonem by byly odkázány na
gravitační manévry.
