Podzim 2020
Základní rovnice popisující chování nabitých částic v EM je Lorentzova rovnice \[ \frac{{\mathrm d}{\bf p}}{{\mathrm d}t} = q\left({\bf E} + {\bf v} \times {\bf B} \right), \]
Je-li přítomné pouze magnetické pole \({\bf B}\) nabitá částice vykonává:
kruhový pohyb, tzv. gyraci v rovině kolmé na \({\bf B}\) a
pohyb podél magnetického pole, který není magnetickým polem ovlivněn.
Střed krouživého pohybu nabité částice se nazývá gyrační střed. Mnohdy je možné zjednotušit popis pohybu částice tak, že se vystředuje přes gyraci a řeší se rovnice popisující pohyb gyračního středu, kde se vlastně žádná částice nenachází.
Ukážeme že přidání elektrického pole způsobí drift gyračního středu ve směru kolmém na \({\bf E}\) a \({\bf B}\).
Podobné driftování gyračního středu způsobí přidání jakékoli síly kolmé na \({\bf B}\), nebo nehomogenita v \({\bf B}\).
Základní příčinou driftů je změna poloměru gyrace při oběhu částice kolem gyračního středu.
Uvažujme statické, homogenní magnetické pole \({\bf B}\) \[\begin{equation} m\frac{{\mathrm d}{\bf v}}{{\mathrm d}t} = q {\bf v} \times {\bf B}, \label{eq:lorentzB} \tag{1} \end{equation}\] za předpokladu \(|{\bf v}|\ll c\), dále předpokladáme, že částice nezáří.
Ukážeme, že magnetické pole nemění kinetickou energii částice
Rovnici \(\eqref{eq:lorentzB}\) vynásobíme \({\bf v}\cdot\) \[
{\bf v}\cdot \frac{{\mathrm d}{\bf v}}{{\mathrm d}t} = q {\bf v}\cdot( {\bf v} \times {\bf B}) \equiv 0
\] protože \({\bf v} \perp ({\bf v} \times {\bf B} )\). Dostaneme
\[ m {\bf v}\cdot \frac{{\mathrm d}{\bf v}}{{\mathrm d}t} = \frac{1}{2} m \frac{{\mathrm d}}{{\mathrm d}t}\left({\bf v}\cdot{\bf v}\right) = \frac{1}{2} m \frac{{\mathrm d}}{{\mathrm d}t}\left(v^2 \right) = \frac{{\mathrm d}}{{\mathrm d}t}\left( \frac{1}{2}mv^2 \right) = 0 \] Statické magnetické pole tedy nemůže změnit kinetickou energii částice.
Podobný závěr bysme dostali i pro prostorově neuniformní \({\bf B}\).
V čase proměnné \({\bf B}\) pole kinetickou energii může změnit, protože vyvolává vířivé elektrické pole
\[
\frac{\partial {\bf B}}{\partial t} = - \nabla\times{\bf E},
\]
to pak může kopat do nabité částice a měnit jeho energii.
Rozložme vektor rychlosti do složky kolmé a rovnoběžné s \({\bf B}\): \[ {\bf v} = {\bf v}_{\perp} + {\bf v}_{\parallel} \]
Pohybová rovnice se rozpadne na dvě. \[ \frac{{\mathrm d}{\bf v}}{{\mathrm d}t} = \frac{{\mathrm d}{\bf v}_{\perp}}{{\mathrm d}t} + \frac{{\mathrm d}{\bf v}_{\parallel}}{{\mathrm d}t} = \frac{q}{m}\left({\bf v}_{\perp}\times{\bf B} \right) + {\bf 0}, \] tedy \[ \frac{{\mathrm d}{\bf v}_{\parallel}}{{\mathrm d}t} = {\bf 0} \quad \hbox{a} \quad \] \[ \frac{{\mathrm d}{\bf v}_{\perp}}{{\mathrm d}t} = \frac{q}{m}\left({\bf v}_{\perp}\times {\bf B} \right). \label{eq:lorentzB-perp} \tag{2} \] Vidíme že magnetické pole neovlivňuje pohyb podél \({\bf B}\).
Prozkoumejme pohyb kolmý na \({\bf B}\). Uvažme \({\bf B} = (0,0,B) = {\bf \hat{z}}B\). Složky rychlosti \({\bf v}_{\perp}=(v_x,v_y,0)\), \({\bf v}_{\parallel}=(0,0,v_z)\), \({\bf v}_{\perp}\times {\bf B} = (v_y B, -v_x B, 0)\). Rovnice pro pohyb v kolmém směru po složkách pak je \[\begin{gather} m\frac{{\mathrm d}v_x}{{\mathrm d}t} &=& q B v_y \\ m\frac{{\mathrm d}v_y}{{\mathrm d}t} &=& - q B v_x \\ m\frac{{\mathrm d}v_z}{{\mathrm d}t} &=& 0 \end{gather}\]
Tyhle rovnice vyřešíme třeba tak, že je zderivujeme podle času a pak je dosadíme z jedné do druhé. \[\begin{gather} \frac{{\mathrm d}^2 v_x}{{\mathrm d}t^2} + \left(\frac{q B}{m}\right)^2 v_x &=& 0, \\ \frac{{\mathrm d}^2 v_y}{{\mathrm d}t^2} + \left(\frac{q B}{m}\right)^2 v_y &=& 0,\\ \end{gather}\] kde \[\omega_c = \frac{|q| B}{m} \]
je tzv. cyklotronová frekvence. Složky rychlosti pak na čase mají závislost:
\[\begin{gather} v_x &=& \pm v_{\perp} \cos(\mp \omega_c t +\psi) \\ v_y &=& \mp v_{\perp} \sin(\mp \omega_c t +\psi) \\ v_z &=& v_{\parallel} \end{gather}\] kde horní znaménko je pro kladnou částici a dolní znaménko je pro zápornou. \(\psi\) je fáze definující orientaci rychlosti částice v čase \(t=0\). \(v_{\perp} = \sqrt{v_x^2+v_y^2}=|{\bf v}_{\perp}|= const.\)
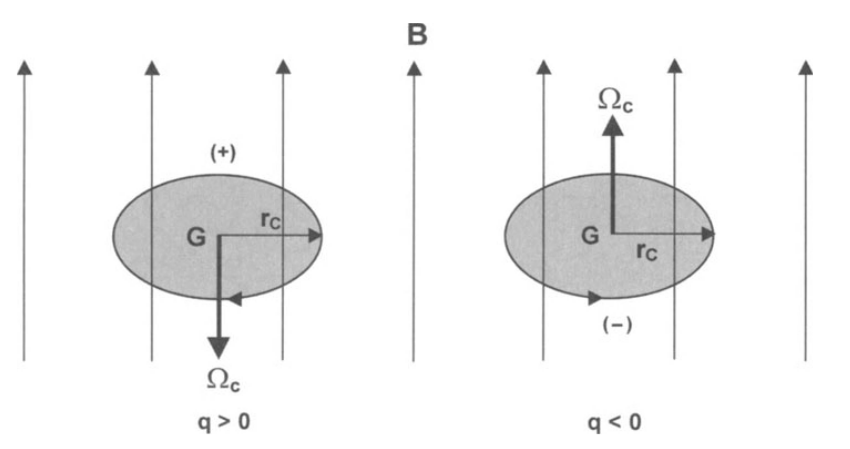
Rovnici \(\eqref{eq:lorentzB-perp}\) je možné formálně přepsat na tvat \[ \frac{{\mathrm d}{\bf v}_{\perp}}{{\mathrm d}t} = {\bf \Omega}_c \times {\bf v}_{\perp}. \label{eq:vperp_omega} \tag{3} \] kde \[ {\bf \Omega}_c = - \frac{q{\bf B}}{m} = \frac{|q|B}{m}{\bf \hat{\Omega}_c} = \omega_c{\bf \hat{\Omega}_c}. \] Jednotkový vektor \({\bf \hat{\Omega}_c}\) směřuje:
ve směru \({\bf B}\) pro negativně nabitou částici (\(q<0\))
proti směru \({\bf B}\) pro kladně nabitou částici (\(q>0\)).
Rovnici \(\eqref{eq:vperp_omega}\) je možné integrovat, uvědomíme-li si že \({\bf v}_{\perp}\,{\rm d}t={\rm d}{\bf r}_c\): \[
{\bf v}_{\perp} = {\bf \Omega}_c \times {\bf r}_c,
\] kde \({\bf r}_c\) je polohový vektor vzhledem ke středu gyrace. Vynásobením této rovnice z leva \({\bf \Omega}_c \times\), s použitím vektorové identity \[
{\displaystyle \mathbf {A} \times (\mathbf {B} \times \mathbf {C} )=(\mathbf {A} \cdot \mathbf {C} )\mathbf {B} -(\mathbf {A} \cdot \mathbf {B} )\mathbf {C} }
\] vyjádříme explicitně vektor \({\bf r}_c\) \[
{\bf r}_c = - \frac{{\bf \Omega}_c \times {\bf v}_{\perp}}{ \Omega_c^2}.
\] Úkol: ověřte že vektor \({\bf r}_c\) má správnou orientaci při gyraci kladné i záporné čístice.
Velikost poloměru gyrační kružnice (tzv. Larmorův poloměr) je \[ r_c =\frac{m v_{\perp}}{|q|B} \]
Vlastnosti gyrace:
\(\omega_c\): nezávisí na rychlosti částice, rychá i pomalá částice oblétne gyrační kružnici za stejnou dobu.
\(r_c\): částice s vyšší rychlostí obíhají po kružnici s větším poloměrem
\(m\): těžší částice gyruje větším \(r_c\) a má delší čas na jeden oběh.
Příklad:
Elektrony: \(\Omega_c = 1.76\times 10^{11} B\) [rad/s]
Ionty: \(\Omega_c = 9.58\times 10^{7} B\) [rad/s]
Magnetické pole země je \(0.5\times10^4\,\)T, pak \(\omega_c/2\pi \sim 1.4\,\) MHz.
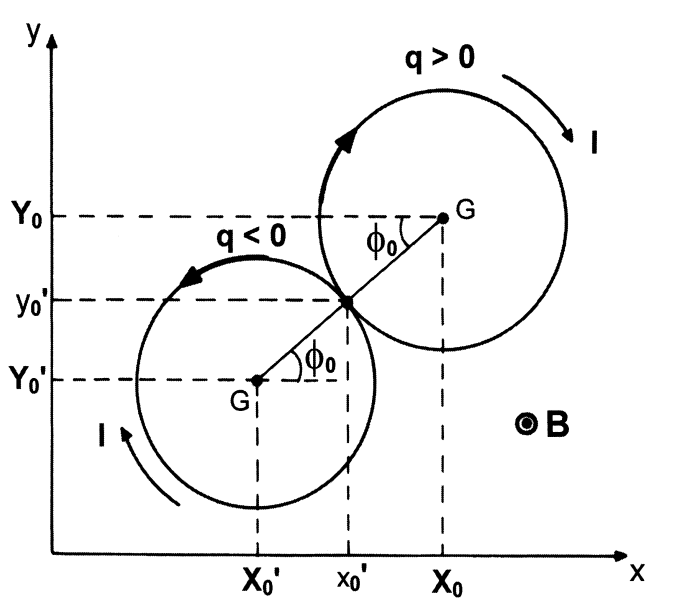
Proud kladné i záporné gyrující částice teče stejným směrem!!! Velikost takového proudu je \[ \left|\frac{q \omega_c}{2\pi}\right| \]
a plocha opsaná gyrující částicí je \(\pi r_c^2\). S tím je spojený magnetický moment \[ \mu = \left(\left|\frac{q \omega_c}{2\pi}\right|\right)(\pi r_c^2)=\frac{mv_{\perp}^2}{2B}. \] Proudová smyčka tvořená gyrující částicí vytváří uvnitř smyčky pole orientované proti magnetickému poli, které gyraci způsobilo. Vektorově: \[ \boldsymbol{\mu} = - \frac{W_\perp}{B^2} {\bf B} \] Magnetický moment gyrující částice je úměrný části kinetické energie, která odpovídá pohybu kolmému k \({\bf B}\) a nepřímo úměrná magnetickému poli, které gyraci vyvolává.
Magnetické pole proudové smyčky je ve velké vzdálenosti ve srovnání s poloměrem \(r_c\) podobné poli magnetického dipólu. Plazma díky tomu jako soubour gyrujících částic vykazuje diamagnetické vlastnosti.
Magnetizace plazmatu je rovna koncentraci gyrujících částic a magnetickému momentu gyrujících částic, (který je úměrný 1/B): \[{\bf M} = n \boldsymbol{\mu}\] Díky této nelineární závislosti (\(\sim1/B\)) magnetizace na magnetickém poli se však plazma jako magnetický materiál většinou nepopisuje.
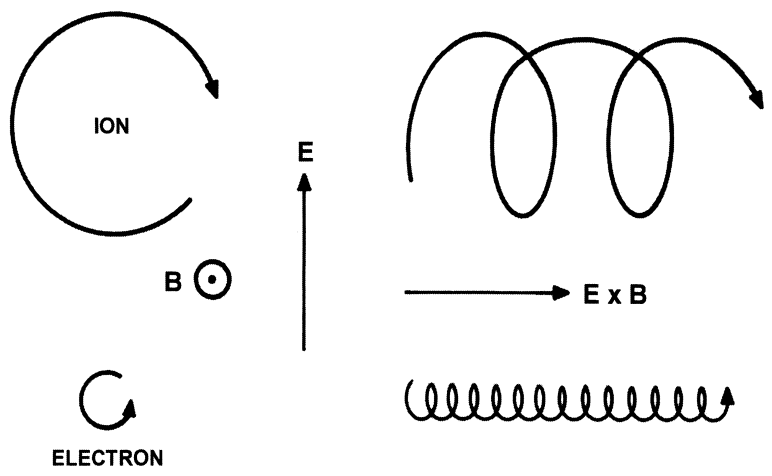
vypustíme-li nabitou (q>0) částici podél elektrického pole, její rychlost se v důsedku elektrické síly bude zvětšovat. Magnetické pole nutí takovou částici, aby se pohybovala po kružnici. Urychlováním se bude ale poloměr kružnice postupně zvětšovat. A to až do okamžiku, kdy se částice začne pohybovat proti elektrické síle. Pak v důsledku jejího zpomalování bude naopak gyrační poloměr klesat až do okamžiku kdy opět vektor rychlosti částice začne mířit podél elektrické síly.
v důsledku změn velikosti rychlosti gyrující částice se deformuje gyrační kružnice a v důsledku této deformace dochází k drifu nabité částice.
Rychlosti \({\bf E} \times {\bf B}\) driftu je stejná pro kladné i záporné náboje. Při absenci srážek elektronů a iontů s neutrály nevyvolává makroskopický proud v plazmatu. V případě, že ke srážkám s neutrály dochází, protože drift iontů je většinou výrazněji srážkami rušen, než drift elektronů, tak makroskopické proudy vznikají. Tento, tzv. Hallův proud je kolmý jak na \({\bf E}\) tak na \({\bf B}\)
Ionty díky své výrazně vyšší hmotnosti gyrují po kružnicích s větším poloměrem než elektrony.
drift probíhá v jedné rovině s gyrací, obrázky nejsou projekce šroubovice!
Uvažujme homogenní magnetické pole \({\bf B}\) a homogenní elektrické pole \({\bf E}\), takové že \({\bf B} \not\parallel {\bf E}\). Rozložme elektrické pole \(E\) a rychlost \({\bf v}\) na část, která je rovnoběžná s \({\bf B}\) a na část, která je kolmá na \({\bf B}\). \[ {\bf E} = {\bf E}_{\parallel} + {\bf E}_{\perp} \]
\[ {\bf v} = {\bf v}_{\parallel} + {\bf v}_{\perp} \]
Lorentzova rovnice se nám rozpadne na část popisující pohyb podél \({\bf B}\) \[
m\frac{{\mathrm d}{\bf v}_\parallel}{{\mathrm d}t} = q {\bf E}_\parallel
\] a na pohyb v rovině kolmé na \({\bf B}\) \[
m\frac{{\mathrm d}{\bf v}_\perp}{{\mathrm d}t} = q({\bf E}_\perp+{\bf v}_\perp\times{\bf B}).
\] Vektor rychlosti \({\bf v}_\perp\) rozložme na část která je v čase neměná (\({\bf v}_{E}\)) a část která se mění \({\bf v}_\perp^\prime(t)\): \[
{\bf v}_\perp(t) = {\bf v}_{E} + {\bf v}_\perp^\prime(t)
\] Dostaneme \[
m\frac{{\mathrm d}{\bf v}_\perp^\prime}{{\mathrm d}t} =
q\left( -\frac{({\bf E}_\perp\times{\bf B})\times {\bf B}}{B^2}
+ {\bf v}_{E} \times {\bf B} + {\bf v}_\perp^\prime \times {\bf B}\right),
\] kde jsme chytře vyjádřili \({\bf E}_\perp\) pomocí sebe sama a vektrou 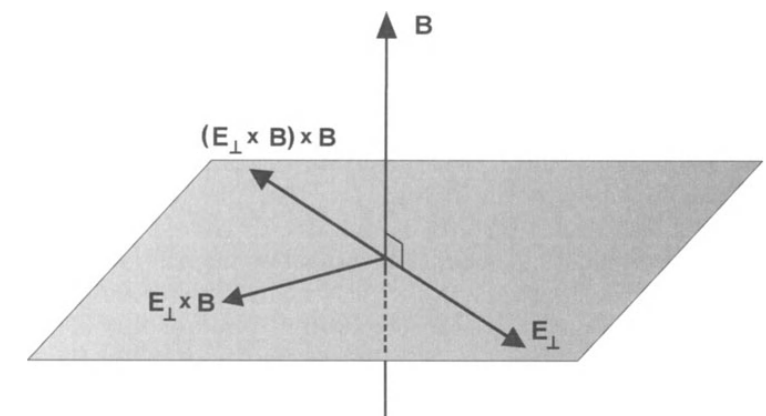\({\bf B}\). 
Přejdeme-li totiž do souřadnicového systému, pohybujícího se konstatní rychlostí \[
{\bf v}_E = \frac{{\bf E}_\perp\times{\bf B}}{B^2},
\] pak časově proměnná \({\bf v}_\perp^\prime\), nepředstavuje nic jiného než prostou gyraci: \[
m\frac{{\mathrm d}{\bf v}_\perp^\prime}{{\mathrm d}t} = q( {\bf v}_\perp^\prime \times {\bf B}).
\]
Pohyb nabité částice v homogením elektrickém a magnetickém poli je tedy superpozicí gyrace a pohybu konstantní rychlostí \[ {\bf v}_E = \frac{{\bf E}_\perp\times{\bf B}}{B^2}, \] ve směru kolmém na \({\bf E}\) a \({\bf B}\). Protože \({\bf E}_\parallel\times {\bf B} \equiv 0\), můžeme rychlost driftu psát jednoduše pomocí \({\bf E}\) \[ {\bf v}_E = \frac{{\bf E}\times{\bf B}}{B^2}. \]
Driftová rychlost \({\bf v}_E\) nezávisí na znaménku náboje, drift je tedy ve stejném směru jak pro elektrony, tak pro ionty.
Místo síly elektrického pole \({\bf F}_E = q{\bf E}\) můžeme uvážit uvážit libovolnou externí sílové pole. Analogicky k \({\bf E} \times {\bf B}\) driftu dostaneme drift způsovený silou \({\bf F}\) \[ {\bf v}_F = \frac{{\bf F} \times {\bf B}}{q B^2} \] Tento drift na rozdíl od \({\bf E} \times {\bf B}\) driftu explicitně závisí na náboji \(q\). Směr driftu bude tedy opačný pro kladné a záporné náboje. Takový drift bude způsobovat makroskopický elektrický proud v plazmatu.
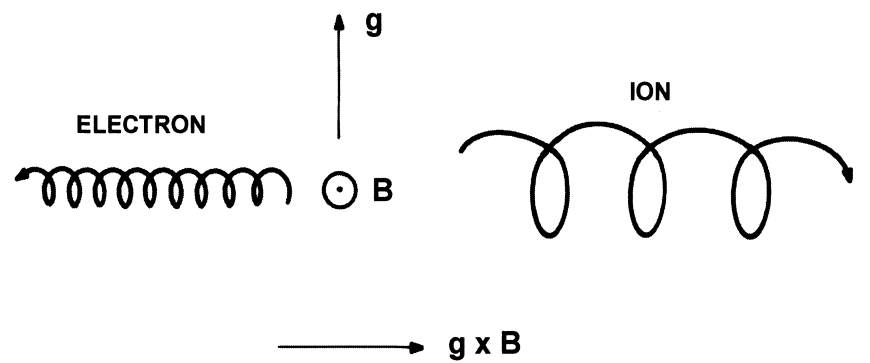
Příkladem síly způsobující drift nabitých částic v plazmatu může být tíhové pole země (tíhové zrychlení \({\bf g}\)). Síla je \[ {\bf F} = m {\bf g} \] a driftová rychlost \[ {\bf v}_g = \frac{m}{q}\frac{{\bf g}\times {\bf B}}{B^2} \]
gravitačí drift závisí na náboji částice
gravitačí drift závisí na hmotnosti částice (ionty budou driftovat mnohem rychleji).
Příklad:
Nabitá částice v magnetickém poli země (při povrchu \(0.5\times10^{-4}\,\)T, ve vakuované komoře), Elektron: gravitační drift \(10^{-6}\) m/s
Proton: gravitační drift \(10^{-3}\) m/s
‘Fair weather’ elektrické pole 100 V/m, magnetické pole \(0.5\times10^{-4}\,\)T
Elektron i proton: \({\bf E} \times {\bf B}\) drift \(10^7\) m/s.
