 Uvažte konstantní koncentraci
\(n_i\) oblaku kladných iontů
zachycených v objemu pasti. Najděte úhlovou frekvenci rotace tohoto
oblaku.
Uvažte konstantní koncentraci
\(n_i\) oblaku kladných iontů
zachycených v objemu pasti. Najděte úhlovou frekvenci rotace tohoto
oblaku.Podzim 2022
\[\begin{align} v_x&=\frac{E_x}{B_z}\sin(\omega_c t),\\ v_y&=\frac{E_x}{B_z}[\cos(\omega_c t) -1],\\ v_z&=\frac{q}{m}E_z t. \end{align}\]
\[\begin{align} x&=\frac{E_x}{B_z\omega_c}[1-\cos(\omega_c t)],\\ y&=\frac{E_x}{B_z\omega_c}[\sin(\omega_c t)-\omega_c t],\\ z&=\frac{q}{2m}E_z t^2. \end{align}\]
\[\begin{align} v_x&=-\frac{E_x}{B_z}\sin(\omega_c t),\\ v_y&=\frac{E_x}{B_z}[\cos(\omega_c t)-1],\\ x&=\frac{E_x}{B_z\omega_c}[\cos(\omega_c t)-1],\\ y&=\frac{E_x}{B_z\omega_c}\sin(\omega_c t) - \frac{E_x}{B_z}t.\\ \end{align}\]
Pohybová rovnice pro částici s nábojem \(q\) a hmotností \(m\)
\[
\frac{{\mathrm d} {\bf v} }{{\mathrm d}t}
= \frac{q}{m}
\left({\bf E}(t) + {\bf v}\times {\bf B}\right)\] rozepsaná po
složkách, s uvážením že \(\omega_c=|q|B/m\): \[\begin{align}
\frac{{\rm d}^2 v_x}{{\rm d} t^2} &+
\omega_c^2\left[v_x - \frac{q}{|q|}
\frac{1}{\omega_c}\frac{\dot{E}_x}{B_z} \right] = 0,\\
\frac{{\rm d}^2 v_y}{{\rm d}t^2} &+
\omega_c^2\left[v_y + \frac{E_x(t)}{B_z} \right] = 0.\\
\end{align}\] Výsledný pohyb částice je tedy superpozice:
– gyrace
– časově závislého ExB driftu \({\bf v}_{ExB} = (0,-E_x(t)/B_z,0)\) a
– a (polarizačního) driftu podél elektrického pole \({\bf v}_p=(+q \dot{E}_x(|q|\omega_c B_z)^{-1},0,0)\). Uvažte konstantní koncentraci
\(n_i\) oblaku kladných iontů
zachycených v objemu pasti. Najděte úhlovou frekvenci rotace tohoto
oblaku.
Uvažte konstantní koncentraci
\(n_i\) oblaku kladných iontů
zachycených v objemu pasti. Najděte úhlovou frekvenci rotace tohoto
oblaku.
Z poissonovy rovnice ve válcové geometrii \[\frac{1}{r}\frac{\partial r E_r}{\partial r} = \frac{e n_i}{\varepsilon_0}\] dostaneme \(E_r = \frac{1}{2}n_i e r \varepsilon_0^{-1},\) Díky ExB driftu oblak iontů rotuje jako těleso úhlovou rychlostí \[\omega=\frac{E}{rB}=\frac{n_i e}{2 \varepsilon_0 B}.\]
Časová změna \({\bf B}\) vyvolá elektrické pole \({\bf E}\), které při gyraci částice koná nenulovou práci. Platí \(W_{\perp} = \mu B\), proto obecně: \[ \frac{{\mathrm d}W_\perp}{{\mathrm d}t} = \mu \frac{{\mathrm d}B}{{\mathrm d}t} + B\frac{{\mathrm d}\mu}{{\mathrm d}t}. \] Změna kinetické energie gyrující částice za jednu gyroperiodu je \[ \Delta W = q \int_0^{T_c} {\bf E}\cdot{{\bf v}_\perp}\,{\rm d}t = q \int_0^{2\pi r_c} {\bf E}\cdot{{\rm d} {\bf l}} \simeq q \oint {\bf E}\cdot{{\rm d} {\bf l}} = - \int (\nabla\times{\bf E})\cdot {\rm d} {\bf S} = - q \int \left( \frac{{\mathrm d}{\bf B}}{{\mathrm d}t} \right) \cdot {\rm d} {\bf S} \] kde \({\rm d} {\bf l}\) a \({\bf S}\), jsou dány směrem pohybu gyrující částice: \({\bf S} \uparrow\!\downarrow{\bf B}\) pro \(q>0\) a \({\bf S} \uparrow\!\uparrow {\bf B}\) pro \(q<0\). Proto \[ \Delta W = - \left(\frac{{\mathrm d}{\bf B}}{{\mathrm d}t}\right)\cdot {\bf S} = + |q|\pi r_c^2 \left(\frac{{\mathrm d}B}{{\mathrm d}t}\right) \] jak pro kladnou tak pro zápornou částici, znaménko \(\Delta W\) bude dáno znaménkem \(\left(\frac{{\mathrm d}B}{{\mathrm d}t}\right)\). Změna za jednu periodu \[ \frac{\Delta W}{T_c} = \frac{{\mathrm d}W_\perp}{{\mathrm d}t} = \frac{|q|\pi r_c^2}{T_c} \left(\frac{{\mathrm d}B}{{\mathrm d}t}\right)= \mu\left(\frac{{\mathrm d}B}{{\mathrm d}t}\right) = \mu \frac{{\mathrm d}B}{{\mathrm d}t} + B\frac{{\mathrm d}\mu}{{\mathrm d}t},\] proto musí platit \[ \frac{{\mathrm d}\mu}{{\mathrm d}t}=0. \]
Ukažte, že elektron oscilující v elektrickém poli je vtahován do míst se slabší intenzitou elektrického pole efektivní silou \[ F_p = - \frac{q^2}{2m\omega^2}E_0\left[\frac{{\mathrm d}E_0}{{\mathrm d}x}\right]. \] Návod: nehomogenitu v elektrickém poli uvažujte jako poruchu, vystředujte přes neporušený oscilační pohyb elektronu s uvážením nehomogenního \(E\) pole.
Vysvětlete fyzikálně tento jev bez použití matematiky.
Pohybová rovnice elektronu je \[ \ddot x = \frac{q}{m}E_a(x)\cos(\omega t). \] 1. krok: pohyb elektronu v neporušeném poli. Řešení pro pohyb elektronu s počáteční podmínku \(x(0)=0,\) \(v_x(0)=0\) bez poruchy pole \((E_a(x)=E_0)\) je \[ x_1(t) = -\frac{qE_0}{m\omega^2}(\cos(\omega t)-1). \] 2.krok: výpočet střední síly působící na elektron za jednu periodu. Střední síla za periodu \(T_p=2\pi/\omega\) s uvážením nehomogenity pole bude \[ \left\langle F_x \right\rangle= \left\langle m \ddot x \right\rangle= \frac{1}{T_p} \int_0^{T_p} q\left(E_0 + x_1(t)\left[\frac{{\mathrm d}E_0}{{\mathrm d}x}\right] \right)\cos(\omega t) \, {\rm d} t.\] Po integraci dostaneme \[ \left\langle F_x \right\rangle=- \frac{q^2}{2m\omega^2}E_0\left[\frac{{\mathrm d}E_0}{{\mathrm d}x}\right]. \] Elektron je tedy vtahován do míst se slabším pole.
Částice bude driftovat \(E\times B\) driftem. Její maximální kinetická energie bude \(2m E^2/B^2\).
Ampérův zákon \[ \oint {\bf B}\cdot {\rm d} {\bf l} = \mu_0 I. \] Pro \(r<a\) dostaneme \[ B(r) = \mu_0 I\frac{r}{2\pi a^2}, \] pro \(r>a\) dostaneme \[ B(r) = \frac{\mu_0 I}{2\pi r}, \]
\[B(r) = \mu_0 j_0\left(\frac{r}{2}-\frac{r^3}{4a^2}\right).\]
\[B(z) = \frac{\mu_0}{2}\frac{I R^2}{(R^2+z^2)^{3/2}},\] \[B_m/B_0 = 1.48, \] \[ \theta_m = 55.3^\circ.\]
Maxwellovy rovnice ve vakuu \[\begin{align} &\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}, \tag{1} \\ &\nabla \cdot \mathbf{B} = 0, \tag{2} \\ &\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}, \tag{3} \\ &\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}. \tag{4} \end{align}\] Aplikací divergence na ronvici (4): \[ \nabla \cdot (\nabla \times \mathbf{B}) = \nabla \cdot \left( \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right) \] s využitím identity \(\nabla \cdot (\nabla \times \mathbf{B} ) = 0\), dostaneme \[ 0 = \nabla \cdot \mathbf{J} + \epsilon_0 \frac{\partial}{\partial t} (\nabla \cdot \mathbf{E}).\] Dále dosazením z rovnice (1) za \(\nabla\cdot \mathbf{E}\) \[0 = \nabla \cdot \mathbf{J} + \frac{\partial \rho}{\partial t},\] dostaneme rovnici kontinuity vyjadřující lokální zachování elektrického náboje: \[\frac{\partial \rho}{\partial t} + \nabla \cdot \mathbf{J} = 0.\]
Ampèrův zákon vynásobíme skalárně s \(\mathbf{E}\) \[\mathbf{E} \cdot (\nabla \times \mathbf{B}) = \mathbf{E} \cdot \left( \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right)\] a roznásobením pravé strany máme \[\mathbf{E} \cdot (\nabla \times \mathbf{B}) = \mu_0 \mathbf{J} \cdot \mathbf{E} + \mu_0\varepsilon_0 \frac{\partial}{\partial t} \left( \frac{1}{2}E^2 \right) \tag{1}\]
Faradayův zákon vynásobíme skalárně s \(\mathbf{B}\) \[\mathbf{B} \cdot (\nabla \times \mathbf{E}) = -\mathbf{B} \cdot \frac{\partial \mathbf{B}}{\partial t} = -\frac{\partial}{\partial t} \left( \frac{1}{2}B^2 \right) \tag{2}. \]
Odečtením (2) od (1) a dostaneme \[\begin{align} \mu_0 \mathbf{E} \cdot \mathbf{J} + \mu_0 \frac{\partial}{\partial t} \left( \frac{ \varepsilon_0 E^2}{2} + \frac{B^2}{2 \mu_0} \right) &= \mathbf{E} \cdot (\nabla \times \mathbf{B}) - \mathbf{B} \cdot (\nabla \times \mathbf{E}) \\ &= (\nabla \times \mathbf{B}) \cdot \mathbf{E} - (\nabla \times \mathbf{E}) \cdot \mathbf{B} \\ &= \nabla \cdot (\mathbf{E} \times \mathbf{B}) \tag{3} \end{align}\] kde jsme použily identity \[ \mathbf{A} \cdot (\nabla \times \mathbf{B}) = (\nabla \times \mathbf{B}) \cdot \mathbf{A}\] a \[{\displaystyle \nabla \cdot \left(\mathbf {A} \times \mathbf {B} \right)=(\nabla \times \mathbf {A} )\cdot \mathbf {B} -(\nabla \times \mathbf {B} )\cdot \mathbf {A} }.\] Úpravou rovnice (3) dostaneme hledaný tvar zákona zachování energie elektromagnetického pole \[ \frac{\partial}{\partial t} \left( \frac{\epsilon_0 E^2}{2} + \frac{B^2}{2 \mu_0} \right) + \nabla \cdot \left( \frac{1}{\mu_0} \mathbf{E} \times \mathbf{B} \right) = - \mathbf{J} \cdot \mathbf{E}, \] nebo \[ \frac{\partial u }{\partial t} = - \nabla\cdot \mathbf{S} -\mathbf{J} \cdot \mathbf{E} . \]
Tato rovnice ukazuje, že rychlost změny hustoty elektromagnetické energie \(u\) je rovna záporné divergenci Poyntingova vektoru \(\mathbf{S}\) minus práci vykonané elektrickým polem na nábojích, která je reprezentována členem \(\mathbf{J} \cdot \mathbf{E}\).
Integrací, z definice (a) \(\sigma_t = 4\pi \sigma_0\), (b) \(\sigma_m = 4\pi \sigma_0.\)
Rozborem srážky tuhých koulí: \[ \frac{{\mathrm d}\sigma}{{\mathrm d}\Omega}=\frac{R^2}{4}. \]
Rozptyl do všech směrů je stejně pravděpodobný (elastický rozptyl elektronu na neutrálním atomu bude izotropní).Bude pokračovat….
Viz přednáška
\[K_0 = \frac{n_0}{8v_0^3}.\]
Populace iontů vznikajících v tokamaku má slowing-down rozdělovací funkci rychlostí: \[ f({\bf v}) = \begin{cases} \frac{\displaystyle A}{\displaystyle v^3+v_c^3}, & \text{pro } \quad v \leq v_b \\ 0, & \text{pro } \quad v > v_b \\ \end{cases} \] kde \(v_b\) je rychlost, kterou ionty mají při svém vzniku a \(v_c\) je konstanta, která je určená frekvencí srážek. Stanovte konstantu \(A\), je-li koncentrace iontů \(N_i\) a určete nejpravděpodobnější rychlost iontů. Najděte odpovídající rozdělovací funkci pro energii iontů.
\[A = \frac{3 N_i}{\displaystyle 4\pi \,\mathrm{ln}\left(1+\frac{v_b^3}{v_c^3}\right)} \] \[v_{mp} = 0\] \[f_E(E) = \frac{3N_i}{2\,\mathrm{ln}\left(1+\left(\frac{\displaystyle E_b}{\displaystyle E_c}\right)^{3/2}\right)} \frac{\sqrt{E}}{E^{3/2}+E_c^{3/2}}\,{\cal H}(E_b-E),\] kde \[ {\cal H}(x)= \begin{cases} 1, & \text{pro } x > 0 \\ 0, & \text{pro } x\leq 0 \\ \end{cases} \]
\(\,\!\)(a) určete konstantu \(C\), (b) ze znalosti rozdělovací funkce rychlostí určete rozdělovací funkci pro velikost rychlosti, (c) najděte nejpravděpodobnější velikost rychlosti, (d) vypočtěte střední velikost rychlosti, (e) najděte tok částic z jedné strany na druhou.
\(\,\!\)(a) určete konstantu \(C\), (b) ze znalosti rozdělovací funkce rychlostí určete rozdělovací funkci pro velikost rychlosti, (c) najděte nejpravděpodobnější velikost rychlosti, (d) vypočtěte střední velikost rychlosti, (e) najděte tok částic z jedné strany na druhou.
Funkci \(g\) přímo dosadíme do Vlasovovy rovnice.
Integrací Vlasovovy rovnice přes celý fázový prostor a použitím per-partes.
Elektrony držené v systému dvou koaxiálních magnetických zrcadel jsou popsány rozdělovací funkcí tvaru \[ f({\bf v}) = \frac{n_0}{\pi^{3/2}\alpha_\perp^2\alpha_\parallel} \left(\frac{v_\perp}{\alpha_\perp}\right)^{\!2} \exp\left( -\left(\frac{v_\perp}{\alpha_\perp}\right)^{\!2} -\left(\frac{v_\parallel}{\alpha_\parallel}\right)^{\!2} \right), \] kde \(v_\parallel\) a \(v_\perp\) reprezentuje velikost rychlosti ve směru podél a kolmo na osu magnetické nádoby, \(\alpha_\parallel^2 = 2kT_\parallel/m\) a \(\alpha_\perp^2 = 2kT_\perp/m.\) (a) ověřte, že \(n_0\) reprezentuje koncentraci částic. (b) stanovte střední podélnou a střední kolmou energii elektronů. (c) odůvodněte aplikovatelnost tohoto rozdělení na částice držené v magnetické nádobě. (d) načrtněte \(f({\bf v})\) v \(\{v_\parallel, v_\perp\}\) prostoru.
\(\!\) (a) přímý výpočet ukáže, že ok: integrace přes \({\rm d}{\bf v} = 2\pi v_\perp\,{\rm d}v_\perp \,{\rm d}v_\parallel\), \(v_\perp\in \left[0,\infty \right],\) \(v_\parallel\in \left[-\infty,\infty \right],\) (b) \[\varepsilon_\parallel=\frac{kT_\parallel}{2},\quad \varepsilon_\perp=2kT_\perp,\] (c) rozborem únikového kužele mag. zrcadla, (d) náčrtek.
\[\langle\mu\rangle = kT_e/B\]
Použijte Sahovu rovnici \[ \frac{n_i}{n_n}=a\frac{T^{3/2}}{n_i}\exp{ (-\frac{U}{kT})}, \] kde \(a=2.405\times 10^{21}\)m\(^{-3}\)K\(^{-3/2}.\) .. (a) ukažte, že sluneční vítr, tedy elektron protonové plazma o teplotě \(10^{5}\)K a koncentraci \(3.5\times 10^{6}\)m\(^{-3}\), je téměř plně ionizované prostředí. Ionizační potenciál vodíku je \(13.6\)eV. (b) Stanovte stupeň ionizace \(\alpha=n_i/(n_i+n_n)\) za atmosferického tlaku (101 325 Pa) a teplotě 300 K, uvažte, že hlavní složka vzduchu je dusík s ionizačním potenciálem \(14.5\)eV.
… (a) dosadit…, (b) celková koncentrace částic \(n_{tot}=p/(kT)\), z toho koncentrace neutrálů \(n_n=n_{tot} - 2n_i\). Pak \(\alpha = 10^{-122}\).
Výpočtem \(\frac{{\mathrm d}f({\bf x}(t),{\bf v}(t))}{{\mathrm d}t}\).
Aplikací řetězového pravidla pro totální časovou derivaci \(f({\bf r}, {\bf v}, t)\).
Členy ve Vlasovově rovnici potřebujeme napasovat na tvar: \[ \frac{\partial }{\partial t}\int f\,{\rm d}v + \frac{\partial }{\partial x}\int v f {\rm d}v + a \int \frac{\partial f}{\partial v} \,{\rm d}v = \ldots = \frac{\partial n}{\partial t} + \frac{\partial }{\partial x}(nu) = 0 \]
kde \(p = \int m (v-u)^2 f \,{\rm d} v\) je kinetický tlak.
\[ \frac{\partial }{\partial t}[n_\alpha\langle\chi\rangle_\alpha] + \nabla\cdot(n_\alpha\langle\chi{\bf v}\rangle_\alpha) -n_\alpha\langle{\bf a}\cdot\nabla_{\!{\bf v}}\chi\rangle_\alpha= \left[\frac{\delta}{\delta t}\left(n_\alpha\langle\chi\rangle_\alpha\right)\right]_{\rm coll}. \]
\[ \frac{\partial }{\partial t}[n_\alpha\langle\chi\rangle_\alpha] + \nabla\cdot(n_\alpha\langle\chi{\bf v}\rangle_\alpha) - n_\alpha\langle({\bf v} \cdot \nabla ) \chi\rangle_\alpha -n_\alpha\langle{\bf a}\cdot\nabla_{\!{\bf v}}\chi\rangle_\alpha= \left[\frac{\delta}{\delta t}\left(n_\alpha\langle\chi\rangle_\alpha\right)\right]_{\rm coll}. \]
\[ {\rm e} + {\rm M} \overset{k_i}{\longrightarrow} {\rm e } + {\rm e } + {\rm M}^+ \]
\[ {\rm e} + {\rm M^+} + {\rm A} \overset{k_r}\longrightarrow {\rm M} + {\rm A} \]
\[ {\rm e} + {\rm A} + {\rm B}\overset{k_c}\longrightarrow {\rm A^-} + {\rm B} \]
\[ {\rm A^{+}} + {\rm B} \overset{k_t}\longrightarrow {\rm A}+ {\rm B^{+}} \]
\[ {\rm AB} + {\rm C} \overset{k_d}\longrightarrow {\rm A} + {\rm B} + {\rm C} \]
\[ {\rm A^*} \overset{\nu}\longrightarrow {\rm A} + \gamma \]
\[ {\rm e} + {\rm N_2} \overset{k}{\rightarrow} {\rm e} + {\rm N} + {\rm N} \]
A jednotlivé procesy pojmenujte.
Viz přednáška.
Toky elektronů a iontů v plazmatu jsou dány drift difuzní aproximací \[ {\bf \Gamma}_{\!e} = - n_e\mu_e{\bf E} - D_e \nabla n_e, \] \[ {\bf \Gamma}_{\!i} = + n_i\mu_i{\bf E} - D_i \nabla n_i. \] V plazmatickém přiblížení \(n=n_e=n_i\), v nemagnetizovaném případě bude intenzita elektrického pole rovnoběžná s gradientem hustoty, a toky elektronů a iontů se musí rovnat \[ \Gamma_{\!a} = - n\mu_e E - D_e \frac{{\mathrm d}n}{{\mathrm d}x}, \] \[ \Gamma_{\!a} = + n\mu_i E - D_i \frac{{\mathrm d}n}{{\mathrm d}x}. \] Kombinací vyjádříme \[ \Gamma_{\!a} = - \frac{D_i\mu_e+D_e\mu_i}{\mu_e+\mu_i}\frac{{\mathrm d}n}{{\mathrm d}x}, \]
\[ E(x) = - \frac{D_e-D_i}{\mu_e+\mu_i}\frac{1}{n}\frac{{\mathrm d}n}{{\mathrm d}x}. \]
Dosazením linearizované nábojové hustoty \[ \rho(x)=e(n_p-n_e-n_n)\approx e\left(n_{p0} -n_{e0}\left( 1 + \frac{e\phi(x)}{kT_e} + \ldots \right) -n_{en}\left( 1 + \frac{e\phi(x)}{kT_n} + \ldots \right) \right) \] do Poissonovy rovnice dostaneme \[ \phi^{\prime\prime}(x)=-\frac{\rho}{\varepsilon_0} = \frac{e^2n_{e0}\phi(x)}{\varepsilon_0 k T_e}(1+\gamma\alpha_0). \] Jejím řešením je exponenciála, která klesá na charakteristické vzdálenosti \(\lambda_{\rm D}^*\).
Integrací momentové rovnice ve stac. stavu \[ Mu\frac{{\mathrm d}u}{{\mathrm d}x}=-e\frac{{\mathrm d}\phi}{{\mathrm d}x} \quad \longrightarrow \quad \frac{1}{2}Mu^2+e\phi = \textrm{const}. \]
Uvažujeme planární geometrii. Ionty jsou studené a mají všechny stejnou rychlost, na okraji sheathu je jejich rychlost \(u_0\). Ionizace v sheathu je zanedbatelná, elektrony jsou uvažovány s Maxwellovským rozdělením. Najděte podmínku pro rychlost iontů na okraji stěnové vrstvy.
Koncentrace elektronů i iontů na okraji sheathu je \(n_s\), jsou svázány kvazineutralitou plazmatu. Potenciál \(\phi\) na okraji sheathu je nulový. Koncentrace elektronů: \[ n_e(x)=n_s\exp\left( \frac{e\phi(x)}{kT_e} \right) \] Koncentrace iontů kombinací momentové rovnice a rovnice kontinuity \[ n_i(x)=n_s\left[1-\frac{\phi(x)}{\bar\phi}\right]^{-1/2}, \] kde \(\bar\phi = \frac{M u_0^2}{2e}.\) Poissonova rovnice pak je \[ \varepsilon_0 \phi^{\prime\prime}(x) = -e n_s\left[(1-\phi(x)/\bar\phi)^{-1/2} - \exp\left( \frac{e\phi(x)}{kT_e} \right)\right] \] Vynásobením \(\phi^{\prime}(x)\) a integrací od okraje sheathu do obecné polohy \(x\) ve stěnové vrstvě \[ 2n_s e \bar\phi(1-\phi(x)/\bar\phi)^{1/2} + n_s k T_e \exp\left( \frac{e\phi(x)}{kT_e} \right) -\frac{1}{2}\varepsilon_0\left(\phi^{\prime}(x)\right)^2 = 2 n_s e \bar\phi + n_s k T_e, \] kde se využilo toho že potenciál je na okraji sheathu nulový a \(\phi^{\prime}\) je tam zanedbatelná vzhledem k \(\phi^{\prime}(x)\).
Rozvinutím ve \(\phi(x)\) \[\begin{gather} 2 n_s e \bar\phi\left[1-\frac{1}{2}\left(\frac{\phi(x)}{\bar\phi}\right) -\frac{1}{8}\left(\frac{\phi(x)}{\bar\phi}\right)^2-\ldots \right]\\ \quad +n_s k T_e \bar\phi\left[1+\left(\frac{e\phi(x)}{kT_e}\right) +\frac{1}{2}\left(\frac{e\phi(x)}{kT_e}\right)^2 + \ldots \right] \\ \quad - \frac{1}{2}\varepsilon_0\left(\phi^{\prime}(x)\right)^2 = 2n_s e \bar\phi + n_s k T_e \end{gather}\] členy nultého a prvního řádu se vyruší, zbude v druhém řádu \[ \frac{1}{2}\varepsilon_0\left(\phi^{\prime}(x)\right)^2 = \frac{n_s e \phi(x)^2}{2}\left(\frac{e}{k T_e}-\frac{1}{2\bar\phi}\right). \] Pravá strana musí být kladná, proto \[ e\bar\phi\geq \frac{1}{2}k T_e, \] a z toho podmínka pro rychlost: \[ u_0 \geq \sqrt{\frac{kT_e}{M}}. \] Ionty tedy musí v pre-sheathu nabrat alespoň rychlost \(u_0\). V pre-sheathu je tedy nutné nenulové elektrické pole, které ionty urychlí. Koncentrace plazmatu mezi centrální, neporušenou oblastí a rozhraním pre-sheath/sheath bude postupně klesat podle Boltzmannova faktoru.
Uvažujte pohyb iontů ve stacionárním pre-sheatu se srážkami. Ionty v presheatu nevznikají, koncentrace elektronů a iontů je popsána Boltzmannovým faktorem a platí podmínka kvazineutrality. Najděte podmínku pro rychlost iontů vstupujících do stěnové vrstvy. Koncentrace plazmatu v neporušené oblasti je \(n_{e0}\)
Elektrony jsou popsány Boltzmannovým faktorem \[ n_e(x)=n_i(x)=n_{e0}\exp\left( \frac{e\phi(x)}{kT_e} \right). \] Pohybová rovnice iontů \[ m_iv_i\frac{{\mathrm d}v_i}{{\mathrm d}x}+m_i\nu_{mi}v_i=-e\frac{{\mathrm d}\phi}{{\mathrm d}x}. \] Z Boltzmannova faktoru vyjádříme \(\phi(x)\) \[ \phi(x)=\frac{kT_e}{e}\mathrm{ln}\left(\frac{n_i}{n_{e0}}\right) \] S využitím rovnice kontinuity \(n_i v_i = \textrm{const.}\) \[ \frac{{\mathrm d}\phi}{{\mathrm d}x} = - \frac{kT_e}{e}\frac{1}{v_i}\frac{{\mathrm d}v_i}{{\mathrm d}x}. \] Pro zrychlení iontů v pre-sheathu dostaneme \[ \frac{{\mathrm d}v_i}{{\mathrm d}x} = \frac{\nu_{mi}v_i^2}{v_B^2-v_i^2}, \] kde \[ v_B^2=\frac{kT_e}{m_i}. \] Pro \(v_i\leq v_B\) je zrychlení iontů kladné. Rovnice je singulární pro \(v_i =v_B\), singularita vzniká požadavkem kvazineutrality (nepoužili jsme Poissonovu rovnici pro výpočet pole!). Na rozhraní pre-sheath/sheath kvazineutralita přestává platit, ionty se tedy urychlí na \(v_B\), ne více.
Potenciálový spád musí být \[ e\Delta\phi=-\frac{1}{2}M\left(\frac{kT_e}{M}\right) \quad \Longrightarrow\quad \Delta\phi = -\frac{kT_e}{2e}. \]
Srážky budou uspořádaný pohyb iontů zpomalovat, potenciálový rozdíl mezi místem vzniku iontů (středová zóna plazmatu) a okrajem stěnové vrstvy bude muset být větší než \(\frac{kT_e}{2e}\).
Z rovnosti toků nabitých částic na plovoucí objekt, pro Maxwellovské elektrony a Bohmovské ionty \[ \frac{n_s \bar v_e}{4}\exp{\left(\frac{e V_f}{kT_e}\right)}=n_su_B, \] dostaneme
\[ V_f=\frac{k T_e}{e} \frac{1}{2} \mathrm{ln}\left(\frac{2\pi m_e}{M}\right). \]
\(V_f\) je dle očekávání záporné, protože \(m_e < M\).
Koncentrace plazmatu a okraji stěnové vrstvy bude \[ n_s = n_0 \exp\left(-\frac{1}{2}\right), \] Debyeova délka pro koncentraci elektronů \(n_s\) a \(T_e=2\,\)eV je \(\lambda_D \sim 1.4\,\)mm, platí tedy \(\lambda_i \gg \lambda_D\) a sheath je možné uvažovat jako bezsrážkový. Tok iontů pak je \(\Gamma_i = n_s u_B \sim 1.3\times10^{19}\) m\(^{-2}\)s\(^{-1}\). Tok energie iontů: \[ \Gamma_\varepsilon = n_s u_B \left(\frac{1}{2}Mu_B^2\right) \sim 2 \,\textrm{J\,s}^{-1}\, \textrm{m}^{-2}. \]
Uvažujte elektrony o teplotě \(T_{e}\) a záporné ionty o teplotě \(T_{n}\) a studené kladné ionty o hmotnosti \(M\). Kvazineutralita na okraji plazmatu je dána podmínkou \(n_{ps}=n_{es}+n_{ns}.\) Elektronegativita neporušeného plazmatu je popsána parametrem \(\alpha_s=n_{ns}/n_{es}\) a poměr teplot elektronů a negativních iontů je \(\gamma = T_e/T_n.\) Ukažte, že rychlost iontů na okraji stěnové vrstvy \(u_s^*\) je vázána podmínkou \[ u_s^{*} = \sqrt{\frac{kT_e}{M}\frac{(\alpha_s+1)}{(1+\alpha_s\gamma)}}. \]
Vyjádřením hustoty náboje \[ \rho(x)=e\left[ n_{ps}\left(1-\frac{2e\phi(x)}{Mu_s^{*2}}\right)^{-1/2} -n_{es}\exp\left(\frac{e\phi}{kT_e}\right) -n_{ns}\exp\left(\frac{e\phi}{kT_n}\right) \right], \] jednonásobnou integrací Poissonovy rovnice vynásobené \(\phi^\prime(x)\) od hranice sheathu do obecné polohy v sheathu a aplikací okrajových podmínek a rozvojem nelineárních členů do druhého řádu dostaneme \[ \frac{1}{2}[\phi^\prime(x)]^2 = -\frac{e n_{es}\phi(x)^2}{2\varepsilon_0} \left[\frac{\alpha_s+1}{Mu_s^{*2}}-\frac{e}{kT_e}(\alpha_s\gamma+1) \right], \] kde výraz v závorce musí být \(\leq 0\), aby pravá strana byla nezáporná. Z toho plyne hledaný výraz pro \(u_s^{*}\).
Rozložení elektrického potenciálu mezi rovinnou stěnou, kde \(\phi(x=0)=-V_0\), a okrajem plazmatu, kde \(\phi(x=s)=0\), je \[ \phi(x)=-\frac{e n_{i0}}{2\varepsilon_0}(x-s)^2.\] Uvažujte spád napětí \(V_0=200\,\)V a elektronovou teplotu \(T_e=2\)eV. Jaké je rozložení hustoty náboje ve stěnové vrstvě? Ukažte, že tloušťka stěnové vrstvy je přibližně 14 Debyeových délek.
\(\rho(x)=en_{i0}=const.\), elektrony
nejsou ve stěnové vrstvě zastoupeny. \(s=\sqrt{200}\lambda_D\), kde
\[\lambda_D=\sqrt{\frac{\varepsilon_0 k
T_e}{n_{i0}e^2}},\] s předpokladem \(n_{i0}=n_{e0}\) na okraji sheathu.
Použijte Langevinovu rovnici \[ \frac{\partial }{\partial t}{\bf u}_e+({\bf u}_e\cdot\nabla){\bf u}_e = -e({\bf E} +{\bf u}_e\times{\bf B}) - \nu_c m_e{\bf u}_e \] pro výpočet stejnosměrné vodivosti plazmatu. Plazma je v ustáleném stavu, externí síla je dána pouze elektrickým polem.
\[\sigma_0 = \frac{n_e e^2}{m_e\nu_c}\]
Pro elektrony uvažujte rovnici kontinuity s nulovými zdrojovými členy a rovnici pro transport hybnosti, ve které jsou srážky mezi elektrony a neutrály uváženy s konstantní srážkovou frekvencí. Pro malou odchylku v koncentraci elektronů \(n_e^\prime\) od rovnovážné hodnoty \(n_0\) můžeme psát \[ n_e({\bf x},t) = n_0 + n^\prime({\bf x},t). \] Driftovou rychlost elektronů je možné považovat za veličinu prvního řádu a uvažovat pouze skalární tlak elektronů. Systém je bez působené elektrických či magnetických polí. Linearizujte uvažované rovnice, definujte difuzní koeficient a odvoďte rovnici pro \(n^\prime\): \[ \frac{\partial n^\prime}{\partial t}=D_e\nabla^2 n^\prime - \frac{1}{\nu_c}\frac{\partial ^2 n^{\prime}}{\partial t^2}.\] Za jakých podmínek nastane \[ \frac{1}{\nu_c}\frac{\partial ^2 n^{\prime}}{\partial t^2} \ll \frac{\partial n^\prime}{\partial t}? \]
\(\ldots\)
Rovnice kontinuity pro elektrony v dusíkovém plazmatu je \[\frac{\partial n_e}{\partial t} + \nabla\cdot (n_e {\bf u}_e) = S_e,\] kde zdrojový člen \(S_e\) je dán procesem \[ {\rm e} + {\rm N}_2 \overset{k_i}{\longrightarrow} 2{\rm e } + {\rm N}^+_2. \] Najděte řešení rovnice kontinuity v ustáleném stavu. Dále platí \({\bf u}_e=u_e {\bf \hat{x}}\); \(u_e\), \(k_i\) a koncentrance N\(_2\) jsou konstantní.
\[n_e(x)=n_{e0}\exp\left(\frac{k_i n_{{\rm N}_2}}{u_e}x\right).\]
(a) Balanční rovnice pro \(n(t) = n_e(t) = n_i(t)\) zahrnující difuzní ztráty (aproximací difuzních ztrát v rovnici kontinuity pomocí charakteristického difuzního času \(\beta=D_a/\Lambda^2\)) a rekombinační zdrojový člen je \[ \frac{{\mathrm d}n}{{\mathrm d}t}=-\beta n - \alpha n^2. \] Integrací (vhodná substituce je \(y(t)=1/n(t)\)) dostaneme \[\frac{n(t)}{n_0} = \frac{\exp\left(-\beta t\right)} {1+\alpha \beta^{-1} n_0 \left(1-\exp\left(-\beta t\right)\right)}. \] (b) Balanční rovnice \[ \frac{{\mathrm d}n}{{\mathrm d}t} = - \alpha n^2 \] s řešením \[ \frac{n(t)}{n_0} = \frac{1}{1+\alpha n_0 t}. \] (c) Rozvojem \[\exp\left(-\beta t\right) = 1 - \beta t + \ldots\] ve výsledku (a), po časy kdy \[ \beta t \ll 1 \] dostaneme výsledek (b).
Uvažujte rovnici \({\bf J} = \mathbb{S}\cdot {\bf E}\), kde \[ \mathbb{S} = \begin{pmatrix} \sigma_\perp & -\sigma_{\rm H} & 0 \\ \sigma_{\rm H} & \sigma_\perp & 0 \\ 0 & 0 & \sigma_0 \\ \end{pmatrix} \] a kartézské souřadnice takové, že \(E_x=E_\perp\), \(E_y=0\), \(E_z=E_\parallel\) a \({\bf B} = B_0{\bf \hat{z}}\). Ověřte, že v tomto souřadnicovém systému platí \[\begin{gather} J_x=\sigma_\perp E_\perp, \\ J_y=\sigma_H E_\perp, \\ J_z=\sigma_\parallel E_\parallel, \\ \end{gather}\] Nakreslete přehledný obrázek objasňující složky vektorů \({\bf E}\) a \({\bf B}\) a nenulové složky tenzoru vodivosti \(\mathbb{S}\).
\({\bf E} =
(E_\perp,0,E_\parallel)\), \({\bf B} =
(0,0,B_0)\). Ukázat vynásobením \(\mathbb{S}\cdot{\bf E}\). Interpretace
obrázkem 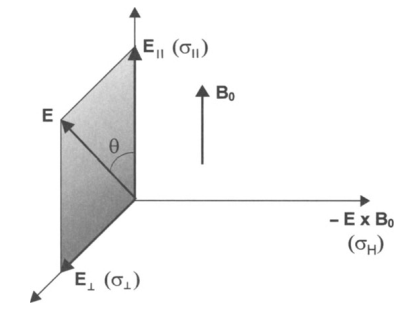
\(\sigma_0\): vodivost podél \({\bf B}\) (\(\parallel {\bf E}_{\parallel}\), \(\parallel {\bf B}\))
\(\sigma_\perp:\) transverzální vodivost (\(\parallel {\bf E}_\perp\), \(\perp {\bf B}\)),
\(\sigma_\parallel\): Hallova vodivost (\(\perp {\bf E}\), \(\perp {\bf B}\)).
\[{\bf J}_\perp = \hat{\bf x}(\sigma_\perp E_x - \sigma_{\rm H} E_y) + \hat{\bf y}(\sigma_{\rm H}E_x + \sigma_\perp E_y) \] \[ {\bf J}_\parallel = \hat{\bf z} \sigma_\parallel E_z\]
Mějme plasma v pevné látce tvořené zápornými elektrony (e) a kladnými děrami (h) o stejné koncentraci. Uvažujme linearizované Langevinovy rovnice \[ m_\alpha\frac{\partial {\bf u}_\alpha}{\partial t} = q_\alpha({\bf E} + {\bf u}_\alpha\times {\bf B}) - \nu_{c\alpha} m_\alpha{\bf u}_\alpha \] pro \(\alpha=\{e,h\}\), \(m_e=m_h\) a \(\nu_{ce}=\nu_{ch}\). Časová závislost \({\bf E}\) a \({\bf u}_\alpha\) je ve formě \(\exp(-i\omega t)\). Použijte kartézské souřadnice s osou \(z\) orientovanou podél konstantního, uniformního magnetického pole \({\bf B}\) a ukažte, že tenzor vodivosti je tvaru \[ \mathbb{S}^* = 2 \begin{pmatrix} \sigma^*_\perp & 0 & 0 \\ 0 & \sigma^*_\perp & 0 \\ 0 & 0 & \sigma^*_0 \\ \end{pmatrix}. \] Určete \(\sigma^*_\perp\) a \(\sigma^*_0\) a vysvětlete proč je Hallova vodivost v tomto případě nulová.
\(\mathbb{S}^* = \mathbb{S}_e + \mathbb{S}_h\), kde \[ \mathbb{S}_e^* = \begin{pmatrix} \sigma^*_\perp & -\sigma^*_{\rm H} & 0 \\ \sigma^*_{\rm H} & \sigma^*_\perp & 0 \\ 0 & 0 & \sigma_0^* \\ \end{pmatrix}, \] \[ \mathbb{S}_h^* = \begin{pmatrix} \sigma^*_\perp & \sigma^*_{\rm H} & 0 \\ -\sigma^*_{\rm H} & \sigma^*_\perp & 0 \\ 0 & 0 & \sigma_0^* \\ \end{pmatrix} \] \[ \sigma_0^*=\frac{e^2n}{m\nu^*} \] \[ \sigma_H = \sigma_0^*\frac{\omega_c\nu^*}{{\nu^*}^2 + \omega_c^2}. \] \[ \sigma_\perp = \sigma_0^*\frac{{\nu^*}^2}{{\nu^*}^2 + \omega_c^2}. \] pro \(\nu^*=(\nu-i\omega)\) a \(\omega_c =|q|B/m.\)
Uvažujte Maxwellovu rovnici \[ \nabla \times {\bf B} = \mu_0{\bf J} + \mu_0\varepsilon_0\frac{\partial {\bf E}}{\partial t} \] a Ohmův zákon ve tvaru \[ {\bf J} = \mathbb S \cdot {\bf E}. \] Ukažte, že pro hamonicky se měnící elektrické pole \(\sim \exp(-i\omega t)\) je dielektrický tenzor plazmatu \[ {\cal E} = \varepsilon_0\left(\mathbb I + \frac{i\mathbb S}{\omega\varepsilon_0}\right), \] kde \(\mathbb I\) je jednotkový tenzor. Najděte složky \({\cal E}\).
Ze struktury \(\mathbb S\) plyne, že dielektrický tenzor \({\cal E}\) je tvaru: \[ {\cal E} = \varepsilon_0 \begin{pmatrix} \epsilon_1 & -\epsilon_2 & 0 \\ \epsilon_2 & \epsilon_1 & 0 \\ 0 & 0 & \epsilon_3 \\ \end{pmatrix}, \] kde \[ \epsilon_1 = 1 + \frac{i}{\omega\varepsilon_0}\sigma_\perp, \] \[ \epsilon_2 = \frac{i}{\omega\varepsilon_0}\sigma_H, \] \[ \epsilon_3 = 1 + \frac{i}{\omega\varepsilon_0}\sigma_0. \]
Uvažujte rovnovážný tok elektronů způsobený gradientem koncentrace: \[ {\bf \Gamma}_e = - D_e \nabla n_e - \frac{e}{m_e\nu_c}({\bf \Gamma}_e\times {\bf B}_0), \] kde \[ D_e=\frac{kT_e}{m_e\nu_c} \] je koeficient volné difuze elektronů. V kartézských souřadnicích s \({\bf B} = B_0{\bf \hat{z}}\) ukažte, že tok elektronů lze vyjádřit ve tvaru \[ {\bf \Gamma}_e = \mathbb D \cdot(-\nabla n_e) \] a najděte složky tenzoru difuze \(\mathbb D\). Jaká je závislost \(D_\perp\) a \(D_H\) na magnetickém poli \(B_0\) pro případ, že gyro-frekvence elektronů \(\omega_c\) je mnohem větší než srážková frekvence \(\nu_c\)?
Postup analogický k výpočtu tenzoru vodivosti \(\mathbb S\). \[ \mathbb D = \begin{pmatrix} D_\perp & -D_H & 0 \\ D_H & D_\perp & 0 \\ 0 & 0 & D_e \\ \end{pmatrix}, \] kde \[ D_\perp = \frac{\nu_c^2}{\nu_c^2+\omega_c^2} D_e, \] \[ D_\parallel = \frac{\nu_c\omega_c}{\nu_c^2+\omega_c^2} D_e. \] gyro-frekvence je \(\omega_c=\frac{e B_0}{m_e}\), \(e\) je kladná konstanta.
Pro silná pole \(D_\perp \propto 1/B_0^2\,\) a \(D_H \propto 1/B_0.\)
Přímým výpočtem v kartézských souřadnicích \[ \frac{\partial n_e}{\partial t}=D_\perp\left(\frac{\partial ^2 n_e}{\partial x^2} + \frac{\partial ^2 n_e}{\partial y^2} \right) + D_e\frac{\partial ^2 n_e}{\partial z^2}. \]
Dvě nekonečné rovnoběžné rovinné desky ve vzájemné vzdálenosti \(2a\) uzavírají mezi sebou plazma o středové koncentraci \(n_0\). Profil koncentrace elektronů mezi deskami je dán stacionárním řešením difuzní rovnice s konstantním difuzním koeficientem \(D_a\), koncentrace na povrchu desek je nulová. V objemu plazmatu dochází k ionizaci s konstantní ionizační frekvencí \(\nu_{ion}.\) Najděte profil koncentrace elektronů \(n(x)\) a potřebnou ionizační frekvenci \(\nu_{ion}\) kompenzující difuzní ztráty.
\[ n(x)=n_0\cos\left(\sqrt{\frac{\nu_{ion}}{D_a}}x\right) \] \[ \nu_{ion} = D_a\frac{\pi^2}{4 a^2} \]
Balanční rovnice popisující ambipolární difuzi nabitých částic v kombinaci s objemovou ionizací je \[ -D_a\frac{{\mathrm d}^2 n}{{\mathrm d}x^2} = n \nu_{ion}. \] Vzhledem k symetrii problému \(n(x)=n(-x)\), pro centrální hustotu elektronů \(n_{e0}\) je řešení ve tvaru \[ n(x)=n_{0}\cos\left(\sqrt{\frac{\nu_{ion}}{D_a}}x\right). \] Z toho tok nabitých částic rekombinujících na stěně \[\Gamma_{\!w}=-D_a\left|\frac{{\mathrm d}n}{{\mathrm d}x}\right|_{a}=n_0\sqrt{\nu_{ion}D_a}\sin\left(\sqrt{\frac{\nu_{ion}}{D_a}}a\right).\] Koncentraci nabitých částic u stěny stanovíme provnáním toku \(\Gamma_{\!w}\) s tepelným tokem nabitých částic na stěnu, se střední rychlostí iontů \(\langle v_i\rangle\) , pro obecné \(\xi<1\) dostaneme \[n_0\sqrt{\nu_{ion}D_a}\sin\left(\sqrt{\frac{\nu_{ion}}{D_a}}a\right) = \xi \frac{n_0\langle v_i\rangle}{4}\cos\left(\sqrt{\frac{\nu_{ion}}{D_a}}a\right).\] Argumenty sinu a cosinu jsou blízké \(\pi/2\), to odpovídá malé kladné koncentraci nabitých částic u stěny, rozvineme je tedy do Taylorovy řady kolem \(\pi/2\) a necháme jen člen prvního řádu \[n_0\sqrt{\nu_{ion}D_a}\left(1-\ldots\right) = \xi \frac{n_0\langle v_i\rangle}{4} \left( \frac{\pi}{2}-\sqrt{\frac{\nu_{ion}}{D_a}} a + \ldots\right).\] Podmínka na udržení výboje pak je \[ \sqrt{\frac{\nu_{ion}}{D_a}} a = \frac{\pi}{2}\left(1+ \frac{4D_a}{\xi a\langle v_i\rangle}\right)^{-1}. \] Difuzní koeficent \(D_a\sim\langle v_i\rangle\lambda_i\), kde \(\langle v_i\rangle\)je střední hodnota rychlosti iontů u stěny a \(\lambda_i\) je střední volná dráha iontů, pak \[ \frac{4D_a}{\xi a\langle v_i\rangle} \sim \frac{4\lambda_i}{\xi a}. \] Je-li splněno \(\lambda_i \ll\xi a\) dostaneme podmínku, která je ekvivalentní předpokladu nulové koncentrace nabitých částic na stěně.
(a) Ambipolární pole je \[ {\bf E}_s = \frac{k_bT_e}{e} \frac{1}{\Lambda} \frac{\sin\left(x/\Lambda\right)}{\cos\left(x/\Lambda\right)} {\bf e}_x. \] (b) Odchylka od neutrality: \[ \delta(x)=\frac{\lambda^2_{D0}}{\Lambda^2}\frac{1}{\cos^3(x/\Lambda)}, \] kde \[ \lambda_{D0}=\sqrt{\frac{\varepsilon_0 k_B T_e}{e^2n_{e0}}} \] je středová Debyeova délka.
Integrací proudové hustoty \[ n_{e0} = \frac{\pi}{4}\frac{I}{e|{\bf u}_e| a D }. \]
Předpokládáme cosinový profil elektronů mezi deskami. Ztráty elektronů jsou ambipolární difuzí na stěny, \(\Lambda=2a/\pi.\) Odpovídající tok elektronů na stěnu je \[ \Gamma_{\!ew} = - D_a \left.\frac{{\mathrm d}n_e(x)}{{\mathrm d}x}\right|_{x=a} = n_{e0}\frac{D_a}{\Lambda}\sin(\pi/2). \] Počet elektronů \(N_e\) ztracený difuzí z výboje za jednotku času z objemu \(S\) desky \[ \frac{{\mathrm d}N_e}{{\mathrm d}t} = \Gamma_{\!ew} 2 S. \] Časová derivace \(N_e\) se dá nahradit poměrem \(N_e\) a charakteristické doby \(\tau\) pro setrvání elektronu ve výboji: \[ \frac{{\mathrm d}N_e}{{\mathrm d}t} \sim \frac{N_e}{\tau} \] \(N_e\) získáme integrací hustoty elektronů přes objem výboje na plochu \(S\). Pak \[ \tau = \frac{\Lambda^2}{D_a}. \]
Balanční rovnice pro elektronovou hustotu s uvážením difúze a ionizace je \[ \frac{\partial n_e}{\partial t} + \nabla\cdot\left(-D_a\nabla n_e \right) = k_i n_0 n_{e}. \] (a) Ve stac. stavu s uvážením pouze jednorozměrné závislosti \(n_e(x)\):
Ve středové oblasti, tj. pro \(x \in [0,a_0]\): \[-D_a\frac{{\mathrm d}}{{\mathrm d}x}\left(\frac{{\mathrm d}n_e}{{\mathrm d}x}\right) = k_i n_0 n_{e0},\] s řešením \[ n_e(x) = n_{e0}\left(1-\frac{k_i n_0}{2 D_a}x^2\right). \] Mimo středovou oblast, tj. pro \(x\in[a_0,a]\): \[ -D_a\frac{{\mathrm d}}{{\mathrm d}x}\left(\frac{{\mathrm d}n_e}{{\mathrm d}x}\right) = 0,\] s řešením \[ n_e(x)=n_e(a_0)\frac{x-a}{a_0-a}. \] Podmínka na spojitost koncentrace elektronů: \[ n_e(a_0) = n_{e0}\left(1-\frac{k_i n_0}{2 D_a}a_0^2\right) \] Podmínka na spojitost toku elektronů: \[ k_i n_0 n_{e0} a_0 = D_a \frac{n_e(r_0)}{a-a_0}. \] (b) Kombinací těchto podmínek dostaneme podmínku na udržení výboje ve tvaru: \[ \frac{D_a}{k_i n_0 a_0^2} = \frac{a}{a_0} - \frac{1}{2}. \]
Válcová trubice s poloměrem \(a\) uzavírá plazma o středové koncentraci \(n_0\). Profil koncentrace elektronů mezi deskami je dán stacionárním řešením difuzní rovnice s konstantním difuzním koeficientem \(D_a\), koncentrace plazmatu na povrchu trubice je nulová. V objemu plazmatu dochází k ionizaci s konstantní ionizační frekvencí \(\nu_{ion}.\) Najděte profil koncentrace elektronů \(n(r)\) a potřebnou ionizační frekvenci \(\nu_{ion}\) kompenzující difuzní ztráty.
Dostaneme rovnici \[ \frac{\partial ^2n}{\partial r^2}+\frac{1}{r}\frac{\partial n}{\partial r}+\frac{\nu_{ion}}{D_a}n = 0, \] která je speciálním případem (pro \(m=0\)) Besselovy rovnice (vyjde jako jedna z rovnic ze separace proměnných v Laplaceově rovnici ve válcových souřadnicích) \[ r^2n^{\prime\prime}+rn^{\prime} + (k^2r^2-m^2)n = 0. \] Jejím řešením je kombinace Besselových funkcí \(J_m(k r)\) a \(Y_m(k r)\): \[ n(r)=A J_m(kr)+B Y_m(k r). \] \(Y_0(r)\) je záporná a singulární pro \(r=0\), řešením tedy bude \(A J_0(kr)\): \[ n(r)=n_0 J_0\left(\sqrt{\frac{\nu_{ion}}{D_a}}r\right). \] Stabilní řešení bude existovat při rovnováze mezi difuzními ztrátami a ionizací: argument funkce \(J_0\) musí být takový aby první kořen byl pro \(r=a\): \[ J_0\left(\sqrt{\frac{\nu_{ion}}{D_a}}a\right)= J_0\left(2.405\right) = 0,\] \(\nu_{ion}\) a \(D_a\) jsou tedy vázány vztahem \[ \nu_{ion} = D_a\left(\frac{2.405}{a}\right)^2. \]
Integrací proudové hustoty \[ n_{e0} = \frac{2.405}{0.5191}\frac{I}{2\pi e|{\bf u}_e| R^2 }. \]
Předpokládáme Besselův radiální profil elektronů. Ztráty elektronů jsou ambipolární difuzí na stěny, \(\Lambda=R/2.405.\) Odpovídající tok elektronů na stěnu je \[ \Gamma_{\!ew} = - D_a \left.\frac{{\mathrm d}n_e(r)}{{\mathrm d}r}\right|_{r=R} = n_{e0}\frac{D_a}{\Lambda}J_1(2.405). \] Počet elektronů \(N_e\) ztracený difuzí z výboje za jednotku času na délku \(L\) trubice \[ \frac{{\mathrm d}N_e}{{\mathrm d}t} = \Gamma_{\!ew} 2\pi R L \] Časová derivace \(N_e\) se dá nahradit poměrem \(N_e\) a charakteristické doby \(\tau\) pro setrvání elektronu ve výboji: \[ \frac{{\mathrm d}N_e}{{\mathrm d}t} \sim \frac{N_e}{\tau} \] \(N_e\) získáme integrací hustoty elektronů přes objem výboje na délce \(L\) trubice. Pak \[ \tau = \frac{\Lambda^2}{D_a}. \]
Poznámka: Frekvence pro únik elektronů z výboje difuzí je \(\tau^{-1}\). Difuzní ztráty se v globálním modelu dají aproximovat touto frekvencí \[ \frac{\partial \tilde n_e}{\partial t} = - \frac{D_a}{\Lambda^2} \tilde n_e, \] kde \(\tilde n_e\) je reprezentativní hodnota elektronové koncentrace ve výbojové trubici.
Balanční rovnice pro elektronovou hustotu s uvážením difúze a ionizace je \[ \frac{\partial n_e}{\partial t} + \nabla\cdot\left(-D_a\nabla n_e \right) = k_i n_0 n_{e}. \] (a) Ve stac. stavu s uvážením pouze radiální závislosti \(n_e\):
Ve středové oblasti, tj. pro \(r \in [0,r_0]\): \[-D_a\frac{1}{r}\frac{{\mathrm d}}{{\mathrm d}r}\left(r\frac{{\mathrm d}n_e}{{\mathrm d}r}\right) = k_i n_0 n_{e0},\] s řešením \[ n_e(r) = n_{e0}\left(1-\frac{k_i n_0}{4 D_a}r^2\right). \] Mimo středovou oblast, tj. pro \(r\in[r_0,R]\): \[ -D_a\frac{1}{r}\frac{{\mathrm d}}{{\mathrm d}r}\left(r\frac{{\mathrm d}n_e}{{\mathrm d}r}\right) = 0,\] s řešením \[ n_e(r)=n_e(r_0)\frac{\mathrm{ln}\left(r/R\right)}{\mathrm{ln}\left(r_0/R\right)}. \] Podmínka na spojitost koncentrace elektronů: \[ n_e(r_0) = n_{e0}\left(1-\frac{k_i n_0}{4 D_a}r_0^2\right) \] Podmínka na spojitost toku elektronů: \[ \frac{k_i n_0 n_{e0}}{2}r_0 = D_a \frac{n_e(r_0)}{\mathrm{ln}\left(R/r_0\right)}\frac{1}{r_0}. \] (b) Kombinací těchto podmínek dostaneme podmínku na udržení výboje ve tvaru: \[ \frac{2D_a}{k_i n_0 r_0^2} = \frac{1}{2} + \mathrm{ln}\left(R/r_0\right). \]
Radiální rozložení koncentrace nabitých částic je \[ n(r)=n_0 \,J_0\!\left(\sqrt{\frac{\nu_{ion}}{D_a}}r\right). \] Tok částic na stěnu difuzí musí být roven tepelnému toku částic: \[\sqrt{D_a\nu_{ion}}\,J_1\!\left(\sqrt{\frac{\nu_{ion}}{D_a}}R\right)= \xi\frac{\langle v_i \rangle}{4}\,J_0\!\left(\sqrt{\frac{\nu_{ion}}{D_a}}R\right). \] Pak \[\frac{4D_a}{\xi\langle v_i \rangle R } x J_1(x) = J_0(x),\] kde \[ x=\sqrt{\frac{\nu_{ion}}{D_a}}R. \] Rozvineme levou i pravou stranu do Taylorovy řady kolem bodu \(x=2.405\), kde má funkce \(J_0(x)\) první kořen: \[ \frac{4D_a}{\xi\langle v_i \rangle R }\left[2.405\,J_1(2.405)+\ldots\right] = \left[-(x-2.405)\,J_1(2.405) + \ldots\right]. \] Podmínka pro udržení stacionárního výboje pak je \[ \sqrt{\frac{\nu_{ion}}{D_a}}R=2.405\left(1-\frac{4D_a}{\xi\langle v_i \rangle R }\right). \] S uvážením \[ \frac{4D_a}{\xi R\langle v_i\rangle} \sim \frac{4\lambda_i}{\xi R}, \] pak je-li splněno \(\lambda_i \ll\xi R\) dostaneme podmínku, která je ekvivalentní předpokladu nulové koncentrace nabitých částic na stěně.
Plně ionizované plazma je popsáno jako jedna tekutina s koncentrací \(n\). Skalární tlak \(p\) je dán součtem tlaku elektronů a iontů \[ p=p_e+p_i=nk(T_e+T_i). \] V rovnovážném stavu gradient tlaku kompenzuje vliv magnetického pole tak, že platí \[ {\bf J} \times {\bf B} = \nabla p,\] kde \({\bf J}\) je celková hustota proudu. Uvažujte zobecněný Ohmův zákon ve tvaru \[ {\bf J} = \sigma_0({\bf E}+{\bf u} \times {\bf B}). \] Ukažte, že pro difuzní tok ve směru kolmém na \({\bf B}\) platí \[ {\bf \Gamma}_\perp = - D^*_\perp \nabla n, \] kde \[ D^*_\perp = \frac{nk(T_e+T_i)}{\sigma_0 B^2}. \] \(D^*_\perp\) je klasický koeficient difuze v plně ionizovaném plazmatu.