Zima 2022
Pro \(n\)-dimenzionální rychlostní prostor uvažme úhly: \[\phi_1, \phi_2, \phi_3,\ldots, \phi_{n-2} \in \left[0,\pi\right]\] \[\phi_{n-1}\in \left[0,2\pi\right]\] a složky rychlostí \(v_i\): \[{\displaystyle {\begin{aligned} v_{1} &= v\cos(\phi _{1})\\ v_{2} &= v\sin(\phi _{1})\cos(\phi _{2})\\ v_{3} &= v\sin(\phi _{1})\sin(\phi _{2})\cos(\phi _{3})\\ & \,\,\,\vdots \\ v_{n-1}&= v\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\\ v_{n} &= v\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1}), \end{aligned}}} \] kde \(v\) je velikost rychlosti.
Element rychlostního prostoru v \(n\)-dimenzích je: \[ {\rm d}^n v = v^{n-1} \sin^{n-2}\phi_1 \sin^{n-3}\phi_2 \ldots \sin\phi_{n-2} \,{\rm d}v \,{\rm d}\phi_1 \,{\rm d}\phi_2\ldots\,{\rm d}\phi_{n-1}, \] z toho dostaneme pro různá \(n\): \[{\rm d}^1 v = v^{0} \,{\rm d}v \] \[{\rm d}^2 v = v^{1} \,{\rm d}v\, {\rm d}\phi_1\] \[{\rm d}^3 v = v^{2} \sin\phi_1\, \,{\rm d}v \,{\rm d}\phi_1\,{\rm d}\phi_2\] \[{\rm d}^4 v = v^{3} \sin^2\phi_1\, \sin\phi_2 \,{\rm d}v \, {\rm d}\phi_1\,{\rm d}\phi_2 \,{\rm d}\phi_3\] \[\ldots\]
Integrací přes všechny úhly dostaneme plochu jednotkové koule v n-rozměrném prostoru. Platí rekurentní formule: \[S_1=2,\quad S_2=2\pi,\quad S_{n}=\frac{2\pi}{n-2}S_{n-2}\] pak \[S_3=4\pi,\quad S_4=2\pi^2,\quad \ldots\]
Nechť \(i\)-tá složka rychlosti má gaussovské rozdělení: \[\frac{g(v_i)}{\tilde n}= \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{v_i^2}{2\sigma^2}\right),\] kde \(\tilde n\) je koncentrace a \[ \sigma=\sqrt{\frac{kT}{m}}.\]
Velikost rychlosti počítaná ze složek je: \[ v=\sqrt{v_1^2+v_2^2+\ldots +v_n^2}. \]
Poznámka: V případě, že rozdělení pro složku rychlosti bude zahrnovat drift \(\mu_i\) \[ \frac{g^{\prime}(v_i)}{\tilde n} = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(v_i-\mu_i)^2}{2\sigma^2}\right) \] je potřeba se nejdříve transformovat do souřadné soustavy pohyující se s driftem, tedy do rychlosti \[ {\bf c} = {\bf v} - {\boldsymbol \mu}, \] ve které se rozdělení rychlostí stane izotropním, jedině pak bude smysluplné provést transpormaci do velikosti rychlosti (a zintegrovat přes všechny směry rychlostí), nebo do energie.
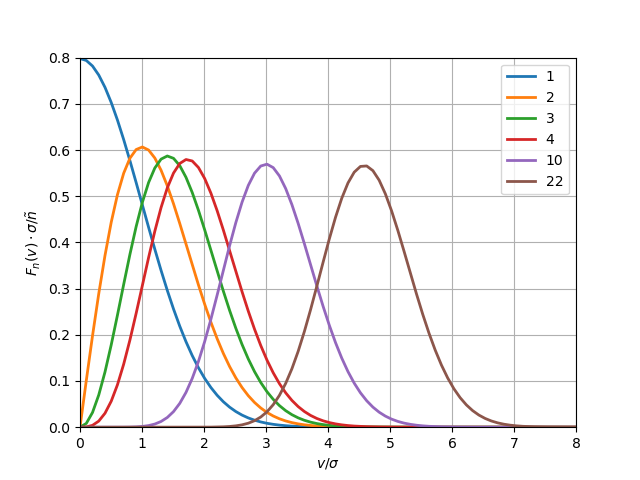
Rozdělení \(F_n(v)\) pro velikost rychlosti v \(n\) rozměrech bude poskládané z násobků rozdělení pro složky rychlosti \[ \frac{F_n(v)}{\tilde n}\,{\rm d}v=\frac{S_n}{{\tilde n}^n} \left(\prod_{i=1}^n g(v_i)\right)v^{n-1} \,{\rm d}v, \] kde \(S_n\) je plocha jednotkové \(n\)-rozměrné koule, která je určena rekurentní formulí uvedenou víše. Explicitní funkční závislost takového rozdělení je \[ F_n(v)\,{\rm d}v = S_n {\tilde n}\left(\frac{1}{\sqrt{2\pi}\sigma}\right)^{\! n}v^{n-1} \exp\left(-\frac{v^2}{2\sigma^2} \right) \,{\rm d}v. \]

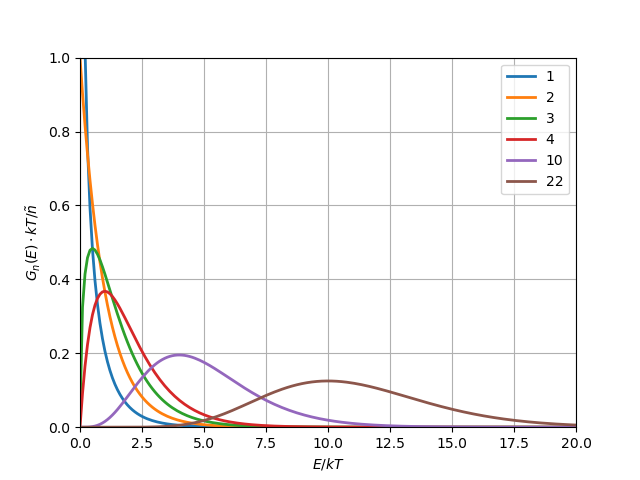
Rozdělení pro energii dostaneme transformací rozdělení \(F(v)\) do energie: \[ E=\frac{1}{2}mv^2 \] Element rychlostního prostoru se transormuje do elementu energiového prostoru jako: \[ {\rm d}v = \frac{{\rm d}E}{(2mE)^{1/2}} \] Použijeme-li \[ \sigma^2 m= kT \] bude rozdělovací funkce pro energii částic v \(n\)-rozměrném prostoru \[ G_n(E)\,{\rm d}E = S_n {\tilde n}\left(\frac{1}{2\pi kT}\right)^{n/2} \exp\left(-\frac{E}{kT}\right)\left(2E\right)^{\frac{n-2}{2}} \, {\rm d}E. \]