


Next: Úkoly:
Up: Základy fotometrie s CCD
Previous: Profil hvězdy
Tvar profilu hvězdy společně s oblohou se dá v prvním přiblížení popsat
některým ze známých analytických profilů jako je Gaussův
(přičemž 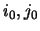 jsou polohy středu hvězdy,
jsou polohy středu hvězdy, 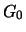 je výška profilu -
základní parametr přímo úměrný dopadající energii hvězdy,
je výška profilu -
základní parametr přímo úměrný dopadající energii hvězdy, 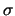 pak
šířka profilu a
pak
šířka profilu a 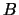 je úroveň
oblohy) nebo Lorentzův:
je úroveň
oblohy) nebo Lorentzův:
My se v dalším přidržíme Gaussova profilu především proto, že má
vhodnější analytické řešení (energie pod profilem je konečná).
Pak lze snadno metodou nejmenších čtverců odhadnout parametry
![\begin{displaymath}
\sum\limits_{i,j} [G(i,j) - D(i,j)]^2 \rightarrow \textrm{min}
\end{displaymath}](img10.png) |
(1) |
přičemž matice 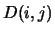 označuje naměřené hodnoty intensit.
označuje naměřené hodnoty intensit.
Filip Hroch
2002-10-21