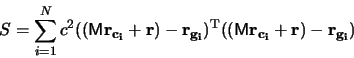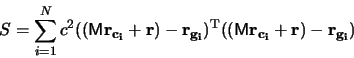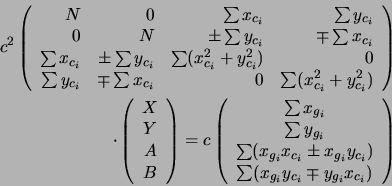Next: Úkoly:
Up: Kalibrace souřadnic snímku
Previous: Lineární transformace
Na odhad parametrů transformace použijeme metodu nejmenších čtverců.
Ke zjištění transformace mezi obrázky pak pro N hvězd
napíšeme součet nejmenších čtverců ve tvaru:
Řešením této podmínky pro neznáme 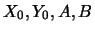 dostáváme
soustavu lineárních rovnic (spodní znaménko pro zrcadlové převrácení):
dostáváme
soustavu lineárních rovnic (spodní znaménko pro zrcadlové převrácení):
pro obecnou transformaci mezi snímky. Tato transformace popisuje
měřítko, posuv, rotaci a zrcadleni mezi obrázky, ale měřítko
je stejné podél osy 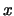 i
i 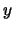 obrázku.
obrázku.
Filip Hroch
2002-11-04