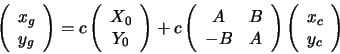Next: Minimalizace
Up: Kalibrace souřadnic snímku
Previous: Gnomonická projekce
Z vlastností gnomonické transformace můžeme usoudit, že obecně budou
mít souřadnice hvězd na CCD snímcích jiné měřítko, budou posunuté
a nebo dokonce pootočené (otočení je vesměs malé a vzniká nedokonalostmi
uchyceni CCD kamery na dalekohledu) oproti souřadnicím vypočteným pro
katalogové hvězdy. Proto pro dobré přiblížení budeme muset použít
ještě dvourozměrnou lineární transformaci. Ta udává vztah mezi
vypočtenými souřadnicemi z gnomonické transformace 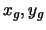 a
měřenými
a
měřenými 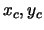 .
.
neboli ve vektorové formě
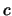 je měřítko.
je měřítko. 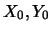 je je relativní posuv mezi snímky.
je je relativní posuv mezi snímky.
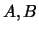 jsou parametry rotace,
jsou parametry rotace, 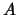 reprezentuje
reprezentuje  a
a
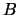 reprezentuje
reprezentuje 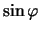 , kde
, kde 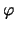 je úhel mezi osami
obrázku (platí goniometrická identita
je úhel mezi osami
obrázku (platí goniometrická identita 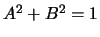 ).
).
Tato transformace nepopisuje zrcadlové převrácení snímku, které
je třeba odhalit jinak.
Měřítko je sice možné odhadnout během minimalizace, ale je zajímavé
si jej odhadnout předem.
Ke zjištění měřítka se používá poměr mezi vzdáleností stejných objektů
jednou na snímku jednou z vypočtených souřadnic. Pro vzdálenost
dvou hvězd na snímcích platí vztah
ze kterého snadno odhadneme měřítko. Z několika známých vzdáleností
pak aritmetickým průměrem dostaneme odhad měřítka v jednotkách pixel
na úhlovou vteřinu (případně naopak).



Next: Minimalizace
Up: Kalibrace souřadnic snímku
Previous: Gnomonická projekce
Filip Hroch
2002-11-04