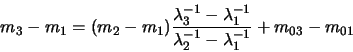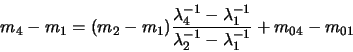Next: Transformace pro VR systém
Up: c4
Previous: Barevné kalibrace
Odvození tvaru transformačních rovnic vychází ze znalosti průběhu
spektra objektu. My budeme předpokládat, že naše měření budeme
provádět pro běžné hvězdy, kdy průběh spektra je dán, až na malé
odchylky představované spektrálními čarami, průběhem spektra
absolutně černého tělesa.
Spektrální průběh intenzity záření takového objektu je dán vztahem:
Přepsání toho vztahu do magnitudové škály vede na vztah:
kde jsme označili
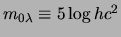 která představuje
posuv nuly a používáme
desítkové logaritmy. V případě, že použijeme dlouhovlnnou aproximaci
při které
která představuje
posuv nuly a používáme
desítkové logaritmy. V případě, že použijeme dlouhovlnnou aproximaci
při které
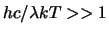 a vypočteme
a vypočteme
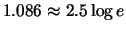 dostaneme
dostaneme
takže pro rozdíl dvou magnitud s vlnovými délkami
 máme
máme
Nyní můžeme začít uvažovat aproximaci pro náš případ. Představme si,
že máme změřené magnitudy nějaké hvězdy ve dvou různých standardních
filtrech o vlnových délkách
 . Dále máme dva filtry
které chceme zkalibrovat o vlnových délkách
. Dále máme dva filtry
které chceme zkalibrovat o vlnových délkách
 které jsou velmi blízké standardním vlnovým délkám (
které jsou velmi blízké standardním vlnovým délkám (
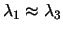 ,
,
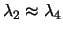 )
a mají velmi podobný
profil spektrální citlivosti. V tom případě můžeme pro tyto standardní
magnitudy psát
)
a mají velmi podobný
profil spektrální citlivosti. V tom případě můžeme pro tyto standardní
magnitudy psát
(nulové členy mají také závislost na vlnové délce ovšem tu v praxi
zanedbáváme). Ze znalosti těchto vztahů můžeme určit alespoň teoreticky
posuvy. V praxi ovšem málokdy známe skutečný posuv ve spektru natolik
přesně jak potřebujeme proto se ty to vztahy přepisují do tvaru
pro magnitudy a do
pro barevné indexy a hodnoty parametrů se pak určují empiricky.



Next: Transformace pro VR systém
Up: c4
Previous: Barevné kalibrace
Filip Hroch
2002-11-25
![]() . Dále máme dva filtry
které chceme zkalibrovat o vlnových délkách
. Dále máme dva filtry
které chceme zkalibrovat o vlnových délkách
![]() které jsou velmi blízké standardním vlnovým délkám (
které jsou velmi blízké standardním vlnovým délkám (
![]() ,
,
![]() )
a mají velmi podobný
profil spektrální citlivosti. V tom případě můžeme pro tyto standardní
magnitudy psát
)
a mají velmi podobný
profil spektrální citlivosti. V tom případě můžeme pro tyto standardní
magnitudy psát