next up previous contents
Next: Dvojhvězdy Up: Počítačové úlohy Previous: Nitro hvězd

Hvězdné atmosféry



Úloha 10.6 Nakreslete graf závislosti poměru koncentrace neutrálního vodíku k celkové koncentraci vodíku v závislosti na teplotě za předpokladu termodynamické rovnováhy. Pro zjednodušení předpokládejte, že koncentrace elektronů je  $ n_{e}=10^{17}\mathrm{m}^{-3}$.

Řešení:    Pro Sahovo rozdělení platí

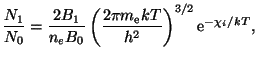
$\displaystyle \frac{N_{1}}{N_0}=\frac{2 B_{1}}{n_e B_0} \left(\frac{2\pi m_\mathrm{e} k T}{h^2}\right)^{3/2}{\mathrm e}^{-\chi_i/kT},$

kde $ N_{1}$ je koncentrace iontu, $ N_0$ neutrálního atomu, $ B_1$ a $ B_0$ jsou příslušné rozdělovací funkce a $ \chi_i$ ionizační potenciál. Celková koncentrace atomů vodíku $ N=N_{1}+N_0$. Pro získání hodnot v grafu je možné použít následující program: 

program sahav;

var tep,nel,x:double;
    i:integer;

function saha(tep,nel:double):double;

const em=9.10956e-31;   {hmotnost elektronu}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      h=6.6256e-34;     {Planckova konstanta}
      exc=13.598;       {excitacni energie H v eV}
      enab=1.6022e-19;  {naboj elektronu}

var b1,b2,x:double;

begin
 b1:=2.0;
 b2:=1.0;
 x:=2.0*pi*em*bolk*tep/h/h;
 saha:=2.0*b2*sqrt(x)*x*exp(-exc*enab/bolk/tep)/nel/b1;
end;

begin
 tep:=1000;
 nel:=1.0e17;
 for i:=1 to 200 do
 begin
  tep:=tep+100.0;
  x:=saha(tep,nel);
  writeln(tep,1.0/(1.0+x));
 end;
end.

Výsledný graf je na obrázku [*].

sahav.epsGraf závislosti relativní koncentrace atomů HI na teplotě. sahav



Úloha 10.7 Nakreslete graf závislosti poměru koncentrace vodíku s elektronem, nacházejícím se na druhé energetické hladině k celkové koncentraci vodíku v závislosti na teplotě za předpokladu termodynamické rovnováhy. Pro zjednodušení předpokládejte, že koncentrace elektronů je  $ n_{e}=10^{20}\mathrm{m}^{-3}$. Vysvětlete tvar získaného grafu. Jaký závěr lze učinit pro čáry Balmerovy série vodíku?

Řešení:    Využijeme výsledku předcházejícího příkladu ([*]) pro výpočet relativního zastoupení neutrálního vodíku. Pro výpočet podílu koncentrace vodíku na druhé hladině k celkovému množství neutrálního vodíku využijeme Boltzmannovy rovnice

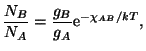
$\displaystyle \frac{N_{B}}{N_A}=\frac{g_B}{g_A}{\mathrm e}^{-\chi_{AB}/kT},$

kde $ N_{B}$ a je koncentrace atomu vodíku na druhé hladině a $ N_A$ celková koncentrace neutrálního vodíku, $ g_B$ a $ g_A$ jejich statistické váhy, $ \chi_{AB}$ excitační energie.

Pro získání grafu na obrázku [*] je možné použít následující program, 

program sahav2;

const em=9.10956e-31;   {hmotnost elektronu}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      h=6.6256e-34;     {Planckova konstanta}
      exc=13.598;       {excitacni energie H v~eV}
      enab=1.6022e-19;  {naboj elektronu}

var tep,nel,x,n,gh,g2,x2:double;
    i:integer;

function saha(tep,nel:double):double;

const em=9.10956e-31;   {hmotnost elektronu}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      h=6.6256e-34;     {Planckova konstanta}
      exc=13.598;       {excitacni energie H v~eV}
      enab=1.6022e-19;  {naboj elektronu}

var g1,g2,x:double;

begin
 g1:=2.0;
 g2:=1.0;
 x:=2.0*pi*em*bolk*tep/h/h;
 saha:=2.0*g2*sqrt(x)*x*exp(-exc*enab/bolk/tep)/nel/g1;
end;

begin
 tep:=1000;
 nel:=1.0e20;
 gh:=2.0;
 n:=2.0;
 g2:=2.0*n*n;
 for i:=1 to 200 do
 begin
  tep:=tep+100.0;
  x:=saha(tep,nel);
  x2:=g2/gh*exp(-exc*enab/bolk/tep*(1.0-1.0/n/n));
  writeln(tep,x2/(1.0+x));
 end;
end.
ve kterém jsme využili funkci saha z předcházejícího příkladu.

sahav2.epsGraf teplotní závislosti relativní koncentrace atomů vodíku na druhé energetické hladině na teplotě.sahav2

Tvar křivky je dán jednak tím, že s rostoucí teplotou roste podíl excitovaných atomů vodíku k atomům v základním stavu. Proto křivka pro nízké teploty zprvu roste. Pro vyšší teploty se začíná vodík ionizovat, ubývá celkového množství atomů vodíku v základním stavu a tedy i podíl atomů vodíku na druhé hladině klesá.

Balmerovy čáry vznikají přechody mezi hladinou s kvantovým číslem $ 2$ a vyššími hladinami. Proto jsou za dané elektronové koncentrace nejvýraznější právě pro teplotu $ T\cong 9800{\rm K}$.



Úloha 10.8 Intenzita vycházející z izotermické vrstvy nacházející se v lokální termodynamické rovnováze je dána přesným řešením rovnice přenosu záření

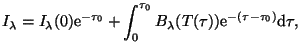
$\displaystyle I_{\lambda}=I_{\lambda}(0){\mathrm e}^{-\tau_0}+ \int_{0}^{\tau_0}B_{\lambda}(T(\tau)){\mathrm e}^{-(\tau-\tau_0)}{\mathrm d}\tau,$

kde $ I_{\lambda}(0)$ je dopadající intenzita záření v bodě s nulovou optickou hloubkou $ \tau=0$, $ \tau_0$ je optická hloubka vrstvy a  $ B_{\lambda}(T(\tau))$ Planckova funkce. V případě zmiňované izotermické vrstvy lze Planckovu funkci vytknout před integrál a provést integraci,

$\displaystyle I_{\lambda}=I_{\lambda}(0){\mathrm e}^{-\tau_0}+B_{\lambda}(T)(1-{\mathrm e}^{-\tau_0})$

Zvolte $ B_{\lambda}(T)=2B_0$ a nakreslete závislost vystupující intenzity na optické tloušťce vrstvy pro hodnoty dopadající intenzity záření $ I_{\lambda}(0)=0,\, 1B_0,\, 2B_0,\, 3B_0$. Diskutujte získané výsledky. Co platí pro opticky tenkou vrstvu ( $ \tau_0\ll 1$) a pro opticky tlustou vrstvu ( $ \tau_0\gg 1$)?

Řešení:    Pro výpočet závislosti vystupující intenzity na tloušťce vrstvy je možné použít následující program: 
program izotv;

var i: integer;
    b,tau,int,i0: double;

begin
 b:=2.0;
 i0:=3.0;
 for i:=1 to 100 do
 begin
  tau:=(i-1)/10.0;
  int:=i0*exp(-tau)+b*(1.0-exp(-tau));
  writeln(tau,int);
 end;
end.
izotv.epsZávislost intenzity vyzářené vrstvou na její optické hloubce pro různé hodnoty dopadající intenzity.izotv Nejprve diskutujme případ, kdy na vrstvu nedopadá žádné záření ( $ I_{\lambda}(0)=0$, viz. obr. [*]). Je patrné, že pro opticky tenké vrstvy je intenzita záření závislá na optické hloubce lineárně, pro rostoucí optické hloubky vrstvy se blíží k Planckově funkci. Obecně, pro libovolnou intenzitu dopadajícího záření platí, že intenzita vystupujícího záření pro případ opticky tenké vrstvy je přibližně rovna intenzitě dopadajícího záření. Příkladem opticky tenkých prostředí mohou být například některé hvězdné větry. Naopak, pro opticky tlustá prostředí intenzita vystupujícího záření se blíží Planckově funkci, nezávisí tedy na intenzitě dopadajícího záření a na optické hloubce vrstvy. Příkladem opticky tlustého prostředí může být sluneční atmosféra v čáře $ \mathrm{H}_{\alpha}$.



Úloha 10.9 Předpokládejte, že nad povrchem hvězdy, který září jako černé těleso o teplotě $ T_p=5\,780\,\mathrm{K}$ se nachází vrstva s optickou hloubkou $ \tau=1$ ve stavu lokální termodynamické rovnováhy. V pozorované oblasti spektra hvězdy se nachází atomární čára, která má střed na vlnové délce $ \lambda_0=500\mathrm{nm}$. S využitím výsledku předcházejícího příkladu vypočtěte pozorovanou relativní intenzitu v závislosti na vlnové délce (vyjádřené v násobcích Dopplerovské šířky čáry  $ \Delta\lambda_D$) v případě, že teplota vrstvy je a)  $ T_v=5\,000\,\mathrm{K}$, b)  $ T_v=7\,000\,\mathrm{K}$, c) $ T_v=T_p$. Přitom položte zdrojovou funkci $ S(\lambda_0,T)=V(a,v)B(\lambda,T_v)$, kde $ V(a,v)$ je tzv. Voigtova funkce s parametry $ v=(\lambda-\lambda_0)/\Delta\lambda_D$ a parametrem $ a$, charakterizujícím Lorentzovské rozšíření čáry (zvolte např. $ a=1$). Voigtovu funkci aproximujte vztahem $ V(a,v)\cong \frac{1}{\sqrt{\pi}}\left(\exp(-v^2)+\frac{a}{\sqrt{\pi}\left(v^2+a^2\right)}\right)$. Vysvětlete získané výsledky.

Řešení:    Pro intenzitu záření černého tělesa je možné odvodit vztah

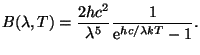
$\displaystyle B(\lambda,T)=\frac{2 h c^2}{\lambda^5}\frac{1}{{\mathrm e}^{hc/\lambda k T}-1}.$

Se znalostí předcházejícího příkladu [*] je možné napsat následující program, který vypočítá záření emitované vrstvou: 
program prof;

const a=1.0;
      tau0=1.0;
      ts=5780.0;
      tl=5000.0;
      lam0=5000.0e-10;

var i,j:integer;
    i0,u:double;
      
function voigt(v,agam:double):double; {Voigtova funkce} 
 begin
  if(abs(v)>8.0) then
    voigt:=agam/sqrt(pi)/(agam*agam+v*v)/sqrt(pi)
   else
    voigt:=(exp(-v*v)+agam/sqrt(pi)/(agam*agam+v*v))/sqrt(pi);
 end;

function b(tep,lam:double):double;

const h=6.6256e-34;     {Planckova konstanta}
      c=2.99792e8;      {rychlost svetla}
      bolk=1.38054e-23; {Boltzmannova konstanta}

var lam5:double;

begin
 lam5:=lam*lam*lam*lam*lam;
 b:=2.0*h*c*c/lam5/(exp(h*c/lam/bolk/tep)-1.0);
end;

function profil(a,tau0,u:double):double;
var tau: double;
begin
 tau:=tau0*voigt(u,a);
 profil:=b(ts,lam0)*exp(-tau)+b(tl,lam0)*(1.0-exp(-tau));
end;

begin
 u:=-10.0;
 i0:=profil(a,tau0,u);
 for i:=0 to 2000 do
  begin
   u:=u+0.01;
   writeln(u,profil(a,tau0,u)/i0);
  end;
end.
profil.epsProfily čar vyzařované vrstvou nacházející se v lokální termodynamické rovnováze pro různé teploty látky.profil

Na obrázku [*] jsou nakresleny profily čar, získané uvedeným programem. Jednotlivým případům uvedeným v zadání se budeme věnovat podrobněji. Obecně však platí (viz. výsledek předcházejícího příkladu [*]), že v centru čáry, kde je optická hloubka vrstvy vysoká, se pozorovaná intenzita blíží Planckově funkci s teplotou rovnou teplotě vrstvy. Naopak v křídlech čáry, kde je optická hloubka vrstvy nízká, se pozorovaná intenzita blíží Planckově funkci s teplotou rovnou teplotě dopadajícího záření. Tento poznatek je také klíčem k pochopení jednotlivých případů. V případě a), kdy je teplota vrstvy nižší než teplota dopadajícího záření, je také hodnota Planckovy funkce v centru čáry nižší, než hodnota Planckovy funkce dopadajícího záření a my pozorujeme absorpční čáry. Tento model je možné použít pro vysvětlení vzniku absorpčních čar např. ve viditelném spektru Slunce. Opačný jev nastává v případě b), kdy je teplota vrstvy vyšší než teplota dopadajícího záření. Tento model popisuje vznik emisních čar. V případě c), kdy je teplota vrstvy rovna teplotě dopadajícího záření se vrstva spolu s okolním zářením nachází ve stavu termodynamické rovnováhy a žádné čáry nepozorujeme.



Úloha 10.10 Pro situaci popsanou v předcházejícím příkladě nakreslete závislost ekvivalentní šířky čáry na optické hloubce čáry.

Řešení:    Pro výpočet ekvivalentní šířky čáry v závislosti na její optické hloubce, je možné využít následující program: 
program krivrust;

const taumin=0.5;
      taumax=100.0;
      ntau=300;
      nlam=200;
      u0=-800.0;
      a=1.0;
      ts=5780.0;
      tl=5000.0;
      lam0=5000.0e-10;

var x,gam: double;
    i,j:integer;
    tau0,w,it,i0,u,dltau,dlam:double;

begin
 tau0:=taumin;
 dltau:=exp((ln(taumax)-ln(taumin))/(ntau-1));
 dlam:=2.0*abs(u0)/nlam;
 for j:=0 to ntau do
  begin
   u:=u0;
   i0:=profil(a,tau0,u);
   w:=0;
   for i:=0 to nlam do
    begin
     it:=(i0-profil(a,tau0,u))/i0;
     u:=u+dlam;
     if(i>0) and (i<nlam) then
       w:=w+it
     else
       w:=w+0.5*it;
   end;
   w:=w*dlam;
   writeln(tau0,' ',w);
   tau0:=tau0*dltau;
 end;
end.

krivrust.epsZávislost ekvivalentní šířky čáry na optické hloubce čáry.krivrust

Funkce voigt, b a profil zde nevypisujeme, všechny je možné převzít z předcházející úlohy [*]. Graf, který byl získán uvedeným programem, je na obr. [*].

next up previous contents
Next: Dvojhvězdy Up: Počítačové úlohy Previous: Nitro hvězd
Jiri Krticka
2002-04-18