Dvojhvězdy

Úloha 10.11 Hvězdy s hmotnostmi $M_1=0,5\,M_{\odot}$ a $M_2=2,0\,M_{\odot}$ obíhají po kruhových drahách kolem společného hmotného středu. Součet poloos obou drah je $a=2.0\,\mathrm{AU}$, inklinační úhel $i=\pi/6$. Nakreslete křivku radiálních rychlostí.

Řešení:    Vzájemná rychlost obou hvězd je dána vztahem $v^2=G(M_1+M_2)/a$, pro radiální rychlost první hvězdy platí $v_{r1}=-\sin i \sin\theta \mu v/M_1$, kde $\theta$ je úhel mezi přímkou spojující hvězdy a směrem k pozorovateli. Pro vykreslení křivky radiálních rychlostí na obr.  lze použít následující program:

radrych.epsKřivka radiálních rychlostíradrych

program radrych;

const au=1.496e11;
      ms=1.989e30;
      a=2.0*au;
      m1=0.5*ms;
      m2=2.0*ms;
      i=pi/6.0;
      ntheta=1000;
      g=6.67e-11;
      rok=60.0*60.0*24.0*365.0;

var si,theta,v,v1,v2,mu,p,t:double;
    j:integer;

begin
 si:=sin(i);
 mu:=m1*m2/(m1+m2);
 p:=2.0*pi*sqrt(a*a*a/g/(m1+m2));
 for j:=0 to ntheta do
 begin
  theta:=2.0*pi*j/ntheta;
  v:=sqrt(g*(m1+m2)/a);
  v1:=-v*mu/m1*sin(theta)*si;
  v2:=v*mu/m2*sin(theta)*si;
  t:=j/ntheta*p/rok;
  writeln(t,' ',v1,' ',v2);
 end;
end.

Úloha 10.12 V případě, že v dvojhvězdě přetéká hmota, je možné rychlost přenosu odhadnout vztahem $\dot M=\rho v A$, kde $\rho$ je hustota látky která přetéká z hvězdy o poloměru $R$ na druhou hvězdu průřezem o ploše $A$. Odhadneme-li plochu jako $A\cong\pi R d$, kde $d$ je tloušťka vrstvy, která přesahuje Rocheovu plochu a rychlost $v$ položíme rovnu tepelné rychlosti, pak rychlost přenosu hmoty je možné odhadnout

$$\dot M \cong\pi R d \rho \left(\frac{3kT}{m_{\mathrm{H}}}\right)^{1/2},$$

kde $k$ je Boltzmannova konstanta, $T$ je teplota a $m_{\mathrm{H}}$ je hmotnost atomu vodíku. Pomocí programu STATSTAR vypočtěte závislost $\dot M$ na $d$ pro hvězdu o sluneční hmotnosti (viz. příklad ).

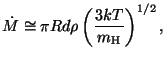
Řešení:    Pro výpočet závislosti rychlosti přenosu hmoty $\dot M$ na tloušťce vrstvy hvězdy, která přesahuje Rocheovu plochu, je možné použít následující program, který načítá model atmosféry (bez hlavičky) vypočtený programem STATSTAR: phmot.epsRychlost přenosu hmoty ve dvojhvězděphmot

program phmot;

const rhv=7.11e8;       {polomer hvezdy}
      rcgs=0.01;        {prepocet CGS}
      rhocgs=1000.0;    {prepocet CGS}
      ms=1.989e30;      {hmotnost Slunce}
      bolk=1.38054e-23; {Boltzmannova konstanta}
      mh=1.6735e-27;    {hmotnost atomu vodiku}


var dm,r,qm,lr,t,p,rho: double;
    i: integer;

begin
 for i:=1 to 424 do
 begin
  readln(r,qm,lr,t,p,rho);
  dm:=pi*rhv*(rhv-r*rcgs)*rho*rhocgs*sqrt(3.0*bolk*t/mh);
  writeln(1.0-r*rcgs/rhv,dm/ms);
 end;
end.