Cvičení Integrování forem F3063

Cvičení se koná v úterý 10.00-11.50 v F2. Další informace o předmětu lze získat v informačním systému.

Materiály

K dispozici jsou příklady vybrané Lenkou Czudkovou.

Zde je vzorová zkoušková písemka a test.

Dále je k dispozici vzorová 1. písemka.

Příklady probírané na cvičení

1. cvičení

Vypočtěte práci, kterou vykoná ideální plyn v jednom Carnotově cyklu.
Je dána lineární transformace \(\alpha\colon V \rightarrow V\) zadaná v bázi \((e_1,e_2,e_3)\) maticí \[ A= \begin{pmatrix} -1 & -6 & 6 \\ -1 & 0 & -1\\ -1 & 3 & -4 \end{pmatrix}. \]
1. Určete bázi v tenzorovém prostoru \(\bigotimes^2 V^*\).
2. V této bázi zapište indukované zobrazení \(\otimes^2 \alpha^* \).
3. Obdobně zapište indukované zobrazení \(\wedge^2 \alpha^* \), určete jeho vlastní hodnoty a formulujte hypotézu v jakém vztahu jsou tyto vlastní hodnoty k vlastním hodnotám původní transformace \(\alpha\).
Je dána množina \(M=\{a,b,c,d\}\). Výčtem otevřených množin zaveďte na \(M\) triviální a diskrétní topologii a ještě jednu topologii odlišnou od předchozích dvou.
Dokažte, že množina \(\mathbf{R}\) s euklidovskou topologií má spočetnou bázi topologie.

2. cvičení

Dokažte, že množina reálných čísel není spočetná. Postupujte následovně:
1. Dokažte, že otevřený interval \((1,2)\) není spočetnou množinou sporem pomocí diagonálního argumentu Georga Cantora.
2. Uvědomte si, že bijekce zachovávají mohutnost množin (tedy i jejich nespočetnost), a zkonstruujte bijekci intervalu \((1,2)\) s reálnou osou.
(Stern-Brocotovy stromy) Každé reálné číslo jednoznačně zobrazte na dvojici racionální číslo a nekonečnou posloupnost ve dvojkové soustavě.
Ukažte, že na každém metrickém prostoru lze definovat topologii.
Dokažte, že otevřené mezikruží v \(\mathbf{R}^2\) s euklidovskou topologií je souvislý topologický podprostor. Uvažte, že na otevřených podmnožinách euklidovských prostorů splývají pojmy "souvislost" a "oblouková souvislost".
Sorgenfreyova topologie je jednou z nestandardních topologií na reálné ose. Báze této topologie je dána \[ \{ [a,b) | a,b \in \mathbf{R}, a< b \}. \] Ubezpečte se, že se jedná o bázi topologie. Ukažte, že touto bází je definována topologie, jež je ostře jemnějsí než euklidovská topologie, tj. že každá otevřená množina v euklidovské topologii je obsažena v Sorgenfreyově topologii a že tyto dvě topologie jsou různé.
Heine-Borelova věta říká, že pro podmnožinu \(U\) v euklidovském prostoru \(\mathbf{R}^n\) jsou následující dvě tvrzení ekvivalentní:
- \(U\) je kompaktní.
- \(U\) je uzavřená a omezená.
Pomocí této věty určete, zda jsou kompaktní následující podmnožiny:
1. \(\{(x,y,z)\in \mathbf{R}^3 | x^2+y^2+z^2\le 1, (x,y,z)\ne (0,0,0)\}\),
2. \(\{(x,y)\in \mathbf{R}^2 | y=x^2, x\ge 0 \}\),
3. \([0,1] \cap \mathbf{Q} \),
4. \(\{ \frac{1}{n} | n\in\mathbf{N}\} \cup \{0\}\),
5. \(\{(x,y,z)\in \mathbf{R}^3 | x^2+y^2\le 1, -1\le z \le 1\}\).
Uvažujte zobrazení \(f \colon \mathbf{R}\rightarrow \mathbf{R}^+_0\), kde reálnou osu i poloosu uvažujeme s euklidovskou topologií, dané předpisem \(x\mapsto x^2\). Je dané zobrazení spojité? Jedná se o bijekci? Má toto zobrazení inverzi? Je tato jeho inverze spojitá?

3. cvičení

Dokažte, že následující množiny mají nulovou Lebesqueovu míru:
1. množina racionálních čísel na reálné ose,
2. přímka v euklidovské rovině,
3. jednotková kružnice v rovině,
4. přímka v prostoru.
Dokažte integrabilitu funkce \(f\colon x \mapsto x^n\), kde \(n\in \mathbf{N}\), na intervalu \([0,1]\).
Dokažte integrabilitu funkce \(f\colon (x,y)\mapsto xy\) na čtverci \([0,1]\times [0,1]\).
Najděte horní a dolní meze u integrálu \(\int_M f(x,y) \mathrm{d} x \mathrm{d} y\):
1. \(M\) je trojúhelník s vrcholy \((0,0), (1,0), (1,1)\),
2. \(M\) je kruhová výseč se středem v bodě \((0,0)\) a vrcholy v bodech \((-1,1)\) a \((1,1)\),
3. \(M\) je úseč paraboly s vrcholem v počátku soustavy souřadnic, s osou splývající s osou \(y\) a vrcholy \((-1,2)\) a \((1,2)\),
4. \(M\) je mezikruží s vnitřním poloměrem \(r=1\) a vnějším poloměrem \(R=2\),
5. \(M\) je oblast ohraničená hyperbolou \(y^2-x^2 =1\) a kružnicí \(x^2+y^2=4\) obsahující počátek soustavy souřadnic.
Spočtěte integrál \(\int_S \mathrm{e}^{\frac{x}{y}} \mathrm{d} x \mathrm{d} y\), kde \(S\) je dáno obrázkem (\(OA\) je část paraboly).
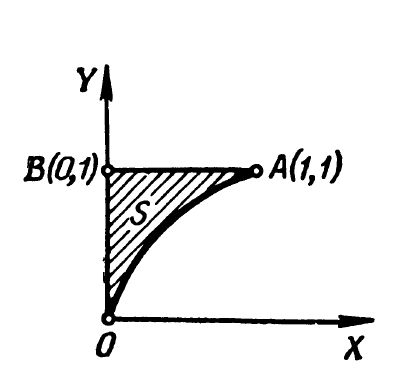
Převodem do polárních souřadnic spočtěte integrál \(\int_S \mathrm{d} x \mathrm{d} y\), kde \(S\) je oblast ohraničená lemniskátou \[ (x^2+y^2)^2= a^2(x^2-y^2). \]

4. cvičení

Přechodem k polárním souřadnicím vyčíslete integrál \[ \int_S (x^2+y^2)\mathrm{d} x \mathrm{d} y, \] kde \(S\) je oblast ohraničená kružnicí \(x^2+y^2=2ax\).
Najděte obsah křivočarého čtyřúhelníka ohraničeného parabolami a hyperbolami \(y^2=ax, y^2=bx\) a \(xy=\alpha, xy=\beta\), \(0 < a < b\), \(0 < \alpha < \beta\).
Spočtěte objem tělesa ohraničeného rovinou \(xy\), dvourozměrnou Gaussovou plochou \(z=\mathrm{e}^{-(x^2+y^2)}\) a válcem \(x^2+y^2=R^2\). Co nastane pro \(R\rightarrow \infty\)?
V jakém poměru rozděluje hyperboloid \(x^2+y^2-z^2 = a^2\) kouli \(x^2+y^2+z^2 \le 3a^2\)?

5. cvičení

Transformujte integrál \[ \int_0^c \mathrm{d} x \int_{\alpha x}^{\beta x} f(x,y) \mathrm{d} y, \] kde \(0<\alpha<\beta\) a \(c>0\), přechodem k novým proměnným \(u=x+y\) a \(uv=y\).
Spočtěte objem \(n\)-rozměrné koule o poloměru \(r\) v \(\mathbf{R}^{n+1}\).
Dokažte, že množina vektorů \(\{v_1,v_2,\ldots,v_n\}\) je lineárně nezávislá, právě když \(v_1\wedge \ldots \wedge v_n \ne 0\).
Vnější algebra v projektivní geometrii v rovině, dualita, incidence a vnější součin.

6. cvičení

Buďte \(V\) a \(W\) vektorové prostory s bázemi \((e_1,e_2,e_3)\) a \((f_1,f_2,f_3,f_4)\). Buď \(\alpha\colon V\rightarrow W\) lineární zobrazení zadané jako \[ \begin{align*} \alpha(e_1)&=f_1-2f_4 \\ \alpha(e_2)&=-f_3 \\ \alpha(e_3)&=f_2+f_4 \end{align*} \] Spočtěte indukovaná zobrazení \(\alpha^*\), \(\wedge^2\alpha\), \(\wedge^2 \alpha^*\), \(\wedge^3\alpha\) a \(\wedge^3\alpha^*\) v indukovaných bazích a určete jejich definiční obory a obory hodnot.
Spočtěte obsah obrazce ohraničeného přímkami \(x-y-1=0\), \(2x-3y+2=0\) a \(x+y-3=0\).
Spočtěte objem tělesa ohraničeného rovinami \(x-y-z-1=0\), \(2x-3y-4z+2=0\), \(x+y+z-3=0\) a \(y-z-1=0\).
Dokažte Cramerovo pravidlo pomocí vnější algebry.
Dokažte Leibnizův vzorec pro výpočet determinantu z definice determinantu lineární transformace \(\alpha \colon V\rightarrow V\) jako \[ \det \alpha e_1\wedge \ldots \wedge e_n = \wedge^n \alpha (e_1 \wedge \ldots \wedge e_n), \] kde \((e_1,\ldots,e_n)\) je libovolná báze ve \(V\).
Dokažte pravidlo pro výpočet determinantu pomocí Laplaceova rozvoje s využitím vnější algebry.
Vnější součin a skalární součin, Hodgeův operátor \(\star\).

7. cvičení

Hodgeův operátor \(\star\) v euklidovském prostoru – pokračování, vyjádření vektorového součinu.
Hodgeův operátor \(\star\) v Minkowského prostoročase.
Kontrakce antisymetrické formy vektorem. Příklad: \[ \alpha = 3 e^1\wedge e^2 \wedge e^4 - e^2\wedge e^3 \wedge e^4 +3 e^1\wedge e^2 \wedge e^3, \quad v= 3e_1-e_2+e_3-2e_4 \] Spočtěte \(\iota(v) \alpha\).
Dokažte následující vlastnosti kontrakce
1. \[ \iota(v) (\alpha \wedge \beta) = \iota(v)(\alpha)\wedge \beta+ (-1)^r \alpha \wedge \iota(v)(\beta), \] kde \(\alpha\in \wedge^r V^*\), \(\beta\in\wedge^s V^*\) a \(v\in V\).
2. \[ \iota(u)(\iota(v)\alpha) = - \iota(v)(\iota(u)\alpha), \] pro \(\alpha\in \wedge^r V^*\) a \(u,v\in V\).

8. cvičení

Vezměme obecnou 1-formu \(\alpha=A(x,y,z)\mathrm{d} x+B(x,y,z)\mathrm{d}y +C(x,y,z)\mathrm{d}z\) v kartézských souřadnicích. Spočtěte \(\star\mathrm{d}\star\alpha\) a rovněž \(\star\mathrm{d}\alpha\).
Spočtěte gradient, divergenci a rotaci vektorového pole ve válcových souřadnicích.
Je dáno zobrazení \(f\colon \mathbf{R}^2 \rightarrow \mathbf{R}^2\) jako \(f(x,y) = (\Re (x+\mathrm{i}y)^2,\Im (x+\mathrm{i}y)^2)\). Spočtěte pullback \((f^{-1})^* (\mathrm{d}x\wedge \mathrm{d} y)\).

9. cvičení

Buď obecněji \(f\colon \mathbf{C}\rightarrow \mathbf{C}\) analytická funkce v komplexní rovině, kterou ztotožníme s \(\mathbf{R}^2\) obvyklým způsobem. Spočtěte pullback \((f^{-1})^* (\mathrm{d}x\wedge \mathrm{d} y)\).
Ukažte, že Laplaceův operátor aplikovaný na vektorová pole (\(1\)-formy) dostaneme jako \[ \Delta \alpha = (\mathrm{d} \star \mathrm{d} \star - \star\mathrm{d} \star \mathrm{d}) \alpha \] tím, že v kartézských souřadnicích dostanete Laplaceův operátor aplikovaný na jednotlivé složky.
Spočtěte gradient, divergenci a rotaci vektorového pole ve sférických souřadnicích. Rovněž spočtěte Laplaceův operátor aplikovaný na funkce i na vektorová pole (\(1\)-formy).
Je dána 1-forma \[ \beta= \frac{-y\mathrm{d}x + x\mathrm{d} y}{x^2+y^2}. \] Zjistěte, zda je \(\beta\) uzavřená, tj. zda je \(\mathrm{d}\beta=0\). Je \(\beta\) exaktní, tj. existuje \(\phi\) tak, že \(\beta=\mathrm{d}\phi\)?

10. cvičení

Laplaceovy operátory v komplexní rovině pomocí komplexních souřadnic.
Konformní invariance Laplaceova operátoru v rovině.
Plošný element v rozšířené komplexní rovině.
1. Napište plošný element na jednotkové sféře určený standardním vložením sféry do \(\mathbf{R}^3\).
2. Zapište inverzní stereografickou projekci, tj. z roviny na sféru.
3. Proveďte pullback touto inverzní stereografickou projekcí plošného elementu na jednotkové sféře.

11. cvičení

Spočtěte integrál \[ \int_C \frac{x \mathrm{d} x + y\mathrm{d} y}{\sqrt{1+x^2+y^2}}, \] kde \(C\) je oblouk elipsy \[ \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 \] umístěný v prvním kvadrantu a orientovaný proti směru hodinových ručiček.
Nalezněte hmotnost povrchu krychle \(0\le x\le 1\), \(0\le y \le 1\), \(0 \le z \le 1\), jejíž plošná hustota je \(xyz\).
Spočtěte integrál \[ \oint_C \frac{(x+y)\mathrm{d} x - (x-y) \mathrm{d} y}{x^2+y^2}, \] kde \(C\) je kružnice \(x^2+y^2=a^2\) orientovaná v kladném smyslu.
Spočtěte integrál \[ \oint_{\partial V} xy \mathrm{d} x \wedge \mathrm{d} y + zx \mathrm{d} z \wedge \mathrm{d} x + yz \mathrm{d} y \wedge \mathrm{d} z, \] kde \(V\) je libovolná oblast v \(\mathbf{R}^3\).
Spočtěte přímo i pomocí Stokesovy věty integrál \[ \int_S x \mathrm{d} y \wedge \mathrm{d} z + y \mathrm{d} z \wedge \mathrm{d} x + z \mathrm{d} x \wedge \mathrm{d} y, \] kde \(S\) je vnější část jehlanu omezeného rovinami \(x=0\),\(y=0\),\(z=0\) a \(x+y+z = a\).

12. cvičení

Spočtěte \[ \oint_C y \mathrm{d} x + z \mathrm{d} y + x \mathrm{d} z, \] kde \(C\) je kružnice \[ \begin{eqnarray} x &=& R \cos \alpha \cos t \\ y &=& R \cos \alpha \sin t \\ z &=& R \sin \alpha \\ \end{eqnarray} \] orientovaná ve směru rostoucího parametru \(t\), přičemž \(\alpha\) je konstantní úhel sklonu roviny kružnice vůči rovině \(z=0.\)
Spočtěte integrál \[ \oint_C \frac{x \mathrm{d} y - y \mathrm{d} x}{x^2+y^2}, \] kde \(C\) je libovolná jednoduchá uzavřená křivka. Uvažte dvě situace: (i) počátek soustavy souřadnic leží uvnitř oblasti ohraničené křivkou, (ii) vně oblasti ohraničené křivkou.
Spočtěte plochu ohraničenou kardioidou; kardioida je množina bodů, kterou opisuje daný bod na kružnici, která se bez prokluzování valí po další kružnici stejného poloměru.
Spočtěte plochu ohraničenou Descartovým listem \(x^3+y^3-3axy=0\), kde \(a>0\).
Spočtěte plochu Cliffordova toru, tj. plochy v \(\mathbf{R}^4\) dané parametricky \[ (r \cos \phi,r\sin\phi,R\cos\theta,R\sin\theta), \] kde \(\phi,\theta\in[0,2\pi)\).
Spočtěte moment setrvačnosti vzhledem k ose \(z\) pro \(n\) závitu šroubovice \[ \begin{eqnarray} x &=& a \cos t \\ y &=& a \sin t \\ z &=& b t.\\ \end{eqnarray} \]
Spočtěte integrál \(\int_S (x^2+y^2) \mathrm{d} S\), kde \(S\) je sféra \(x^2+y^2+z^2=a^2.\)
Zjistěte povrch rotačního paraboloidu \(az = x^2+y^2\), \(a>0\) omezeného rovinou \(z=h\).